非規則網格下二維淺水流動的數值模擬
| 論文類型 | 基礎研究 | 發表日期 | 2002-04-01 |
| 來源 | 《澳門環境城城市發展科學研究》 | ||
| 作者 | 陳祖華,王光謙,王志石 | ||
| 關鍵詞 | 淺水方程有限體積法Roe格式潮流澳門周圍水域 | ||
| 摘要 | 本文建立了一種在非規則結構化網格上求解平面二維淺水流動的有限體積方法,通過采用地形在離散網格內雙線性變化及離散網格界面間地形連續的地形逼近方法,應用可以有效處理間斷問題的 Roe格式來離散淺水方程中的對流項,并通過Van Leer提出的狀態插值法提高格式精度。在計算原始變量在網格內的插值梯度時,采用最小二乘方法求變量的最優梯度代替差分計算梯度,從而可采用任意形狀的不規則四邊形網格離散計算域。計算實例表明,本文的方法能夠計算間斷問題并能夠處理各種復雜流態的過渡,具有較好適應性和計算精度,能夠滿足不同實際問題 | ||
陳祖華 王光謙
(清華大學教育部水沙科學重點實驗室,北京100084)
王 志 石
(澳門大學科技學院,澳門)
摘要:本文建立了一種在非規則結構化網格上求解平面二維淺水流動的有限體積方法,通過采用地形在離散網格內雙線性變化及離散網格界面間地形連續的地形逼近方法,應用可以有效處理間斷問題的 Roe格式來離散淺水方程中的對流項,并通過Van Leer提出的狀態插值法提高格式精度。在計算原始變量在網格內的插值梯度時,采用最小二乘方法求變量的最優梯度代替差分計算梯度,從而可采用任意形狀的不規則四邊形網格離散計算域。計算實例表明,本文的方法能夠計算間斷問題并能夠處理各種復雜流態的過渡,具有較好適應性和計算精度,能夠滿足不同實際問題的計算要求。
關鍵詞:淺水方程有限體積法Roe格式潮流澳門周圍水域
1.引言
許多工程中的流動問題常常可以用淺水流動模型來描述,如近海、湖泊、水庫及河日中的流動。由于應用廣泛,對淺水流動控制方程組的數值方法也受到較多關注。由于淺水方程在數學上屬雙曲方程組,在一定的條件下會產生如水躍。潰壩波、涌浪等的強間斷解,這給方程的數值求解帶來了一些困難,普通的有限差分格式不能有效處理間斷解,因而大大限制了所編制程序的應用范圍。近年來,在計算空氣動力學中已經較為成熟的許多高精度于振蕩的激波捕捉格式,如TVD格式、利用黎曼解的 Godunov型格式等,這些格式克服了間斷產生的數值振蕩,可以處理復雜流態的過渡,正越來越多地被應用到淺水流動計算中,如[1]~[3]。與氣流不同,由于淺水流動存在底部地形的變化,當地形變化較大時不能直接應用這些格式。
本文通過采用地形在離散網格內雙線性變化及離散網格界面間地形連續的地形逼近方法,采用可以有效處理間斷問題的Roe格式[5]來離散淺水方程中的對流項,在此基礎上建立了一種平面二維淺水方程的數值求解方法。采用 Van Leer提出的狀態插值法(MUSCL)[6]問提高格式精度,界面狀態插值時采用了文獻[1]中使用的方法即以對水位插值代替水深插值,以解決在復雜地形條件下應用Roe格式的問題。在計算原始變量在網格內的插值梯度時,本文采用最小二乘方法求變量的最優梯度代替差分計算梯度,從而可采用任意形狀的不規則四邊形網格離散計算域,這避免采用正交曲線坐標變換方法以擬合很多實際問題中計算域的不規則的邊界,降低了網格生成的困難,同時又能具有較高的邊界擬合精度。
2.基本方程
采用如下守恒形式的水深平均平面二維流動控制方程組:
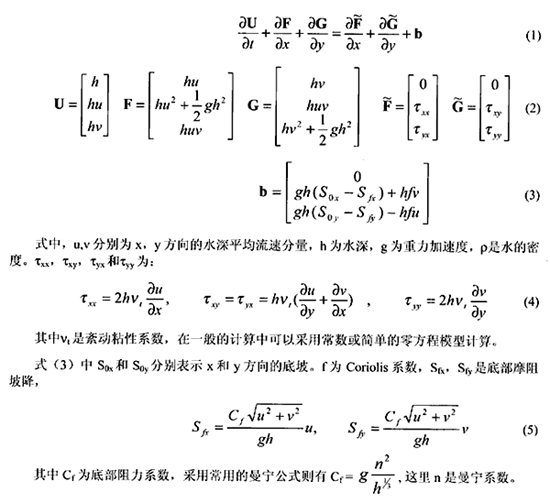
 3.3.數值求解方法
3.3.數值求解方法
本文采用有限體積法求解方程(1)。有限體積法的關鍵在于計算對流通量的格式。考慮到淺水方。程雙曲性和非線性的特點,本采用一種有效處理間斷問題的R。i通量差分裂格式[5],該格式具有自動處理復雜流態過渡,無振蕩等優點,因此本文所用的數值方法不僅適用與一般的光滑流動,也能計算潰壩水流或有水躍等復雜流態過渡的流動問題。采用這種無振蕩的格式也利于在潮汐流動計算中處理活動邊界。由于這種利用黎曼解的格式是中計算空氣動力學推廣而來,因此必須要考慮淺水流動有別于氣流的萬面[7],主要是在淺水流動中要考慮水下為了在水下地形變化較大時也能夠直接推廣應用Roe格式,本文采用任意四邊形網格離散計算域,并假定每一網格內的地面高程雙線性變化,網格間的交界面上底高程保持連續,如圖1所示,這時一個離散網格內的地形分布由其四個頂點的高程決定。
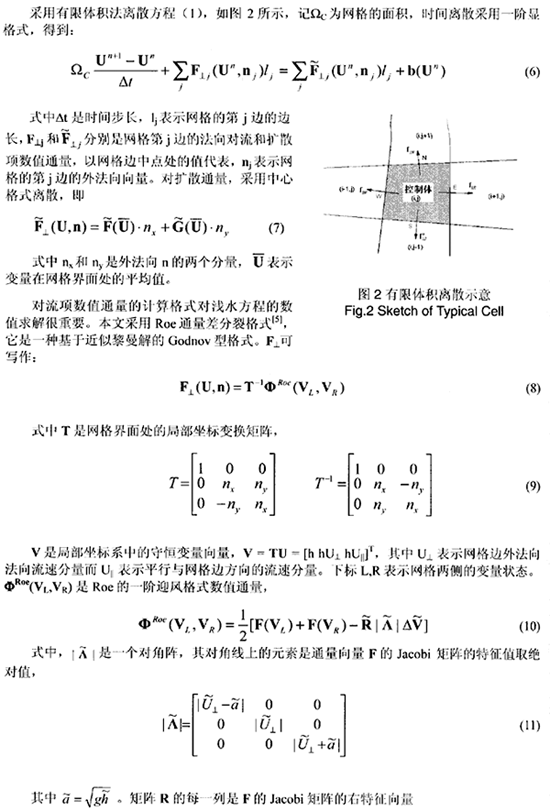

式中 ![]() 采用同樣的方法得到。采用這種方法而不是使用單側差分求變量的變化梯度,雖然計算量和格式數值粘性均有所增加,但是可以采用不規則網格,從而降低了網格生成的困難,又能提高不規則邊界的擬合精度。
采用同樣的方法得到。采用這種方法而不是使用單側差分求變量的變化梯度,雖然計算量和格式數值粘性均有所增加,但是可以采用不規則網格,從而降低了網格生成的困難,又能提高不規則邊界的擬合精度。
但是對于淺水流動來說,由于存在水下地形的變化,有時地形變化還較大,這時采用以上的插值方法不適用,一般的處理方法是將水深插值代以對水位插值,在插值出網格界面中點水位后,減去該點水底高程得到水深[1]。這也是為什么水下地形的描述方式要求保證網格界面地形連續的原因。
4.邊界條件及動邊界處理
采用虛網格法來設置邊界條件,通過把邊界條件加在對應的虛網格上,這樣可以使邊界通量的計算采用與域內相同的方法計算,使邊界格式與內點一致。邊界條件可分為固壁邊界和開邊界兩種。對固壁邊界,法向流速為零而切向常采用滑移條件。其相應的虛網格的變量值采用鏡像條件確定。即具有與內點相同的水深而流速是內點流速關于邊界的鏡像,同時其狀態插值的受限坡度δ 與內點在邊界法向投影大小相等,方向相反[2]。對開邊界虛網格上的未知量,本文采用變量外插來確定。
動邊界問題常常是河口海岸地區數值模擬中需要考慮的,它也是數值計算中一個比較困難的問題。采用Roe格式有利于處理動邊界問題,因為經過修正后的Roe格式已滿足嫡條件且具正性,能夠正確計算有水網格與無水網格界面的數值通量(它實際上是一個下游無水時的潰壩問題),不會因數值振蕩引起負水深導致計算無法進行,無需特別的處理。但是對網格取平均后在動邊界處常常具有偏高的流速,為了保證計算穩定,仍然需要對動邊界作一定的處理。本文采用的方法是將兩側網格都是不完全淹沒網格的網格邊界當作固壁邊界處理以阻止動邊界處的水深擴散,避免較高的流速。這里所謂不完全淹沒指網格形心的水位小于任意一個網格節點的水下高程。這可以看作是小水深法的一種變體,但是它更好地保持了有限體積法的守恒優點。此外,在動邊界附近,為了防止摩阻項引起計算失穩,需要對該項作一些限制,限于篇幅不在此處討論。
5.計算實例與討論
本文采用兩個模型問題和一個實際算例來檢驗所提出的方法。第一個例子是一維潰壩水流的水槽實驗,它檢驗數值格式處理間斷、復雜流態過渡和動邊界的能力;第二個例子是計算Bellos等[9]的二維潰壩水流的水槽實驗,檢驗本文方法處理二維間斷水流計算的效果;澳門周圍水域潮流計算說明本文方法在工程實例中的應用效果。
5.1.一維潰壩水流計算
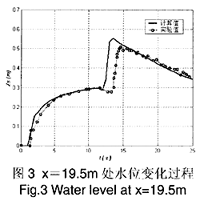
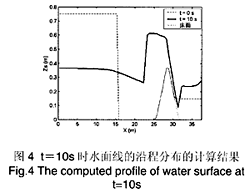
這個例子取自文獻[4]。等寬水槽中設置一個截面為三角形的堰,在距左端 15.5mn處設有閘門,閘門上游水深 0.75m(圖 4中虛線),閘門與堰之間無水。水槽末端為高 0.15m的擋水堰,它與上述三角形堰之間保持 0.15m深的靜水。在在一 0時突然將閘門移去。計算采用均勻網格,空間步長0.5m,計算中對下游邊界作了簡化,沒有考慮末端擋水堰而是將下游看作靜水深 0.15m的無限長渠道。計算中忽略擴散項,曼寧糙率取 0.0125[4]。圖 3是距水槽左端 19.5m處的水位隨時間的變化過程計算值與實驗量測值的比較,二者符合較好。圖 4中實線是t= 10s時水位沿程分布,可以看到在三角形堰前后水流均發生了水躍。除下游段因邊界簡化而與文獻[4]中有所差異外,本文計算的結果與原文獻是一致的。
5.2二維潰壩水流
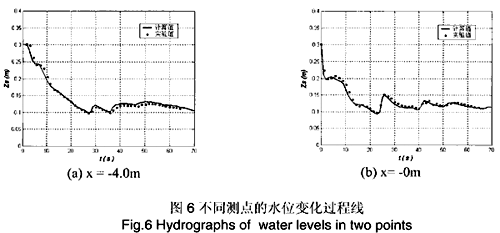
 這個例子是 Bellos等[9]進行的一個瞬時潰壩水流的水槽實驗。實驗水槽如圖5所示。水槽中部有一個收縮.擴散段,閘門位于其中最窄處,瞬時打開。所選的計算條件是上游水深30cm,下游水深10.1cm,底坡為0。計算糙率取0.012,共劃分為42×10個網格,下游末端的邊界條件為矩形薄壁堰的水位流量關系。圖6是幾個測點的水位過程線的計算和實測值的對比,其中X=0指上游緊靠閘門處的測點。由圖可見,各測點的計算值均很好地和實測值符合。
這個例子是 Bellos等[9]進行的一個瞬時潰壩水流的水槽實驗。實驗水槽如圖5所示。水槽中部有一個收縮.擴散段,閘門位于其中最窄處,瞬時打開。所選的計算條件是上游水深30cm,下游水深10.1cm,底坡為0。計算糙率取0.012,共劃分為42×10個網格,下游末端的邊界條件為矩形薄壁堰的水位流量關系。圖6是幾個測點的水位過程線的計算和實測值的對比,其中X=0指上游緊靠閘門處的測點。由圖可見,各測點的計算值均很好地和實測值符合。
5.3.澳門周圍水域潮汐流動的計算
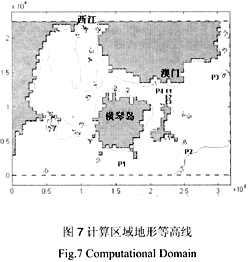
澳門附近水域東臨憐什洋灣日之西側、往西連接磨刀門水道的支汊洪灣水道;南面是珠江口外海區。在上游徑流、外海潮流、沿岸流、風浪流等水動力共同作用影響下,水流運動較為復雜。我們采用上述數值方法對澳門周圍水域的潮汐流動進行一計算,為了利川現有資料,計算采川均勻矩形網格,計算區域為32.0 km × 22.km的 矩形(圖7〕,共劃分為65 ×46個網格,網格人小為 500m × 500m。
采用1980年n月的一組水文資料對澳門周圍水域的潮汐流動作了驗證計算,計算中糙率取0.017。邊界條件的確定方法如下:對南邊界采用水位邊界條件,由實測潮汐水位指定。對西江入口處給定流量,由于資料有限,只能給定一個恒定流量,忽略了時間變化過程。其余開邊界無資料給定,采用人工數值邊界條件。
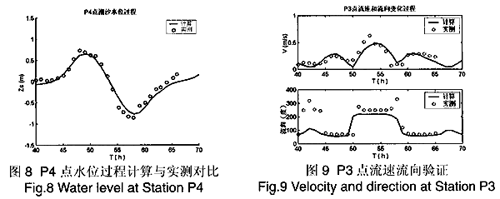
圖8是計算的P4點水位與實測資料的對比。由圖可見漲落潮的潮位、相位和波形均與實測吻合良好,計算基本反映了該地區的潮位變化規律。圖9是P3測點的流速計算值與實測值的對比,兩者較為符合,只是開始幾小時流向誤差較大,這一方面可能是因為在平潮時流速較小,可能的測量誤差較大,另一方面是也可能是因為數值邊界條件未能完全反映來自伶仃洋的潮流的影響造成的誤差。
6.結語
在淺水流動計算中非線性對流項的數值離散格式對計算是非常重要的,本文將基于黎曼解的Roe格式結合MUSCL方法應用平面二維淺水流動的數值計算中,在此基礎上建立了一種數值求解平面二雛淺水流動的數值方法。由于采用最小二乘方法解網格內的最優梯度代替單側差分,本文方法的人工數值耗散較一般TVD格式大,但是可以直接應用于任意不規則的離散網格上而不采用坐標變換,在降低網格剖分要求的同時增加了對物理邊界擬合的精度。計算實例表明,由于采用了性能較好的Roe格式,本文的方法能夠計算間斷問題并能夠處理各種復雜流態的過渡,具有較好適應性和計算精度,能夠滿足不同實際問題的計算要求。
參考文獻:
[1]胡四一,譚維炎,無結構網格上二維淺水流動的數值模擬,水科學進展,1995,6(l):1~9
[2]Bradford S.F.and Katopodes N.D.Hydrodynamics of turbid underflows.I:Formulation andnumerical analysis.Journal of Hydr.Eng., 1999,125(10):1006—1015
[3]蘇銘德,徐昕,朱錦林,韓耀宗,數值模擬在錢塘江涌潮分析中的應用I.數值計算方法,力學學報,1999,31(5):521~533
[4]Garcla-Navarro P.& Vazquez-Cendon M.E.On numerical treatment of the source terms in theshallow water equations,Computers & Fluids,2000,29:951~979
[5]Roe,P..L.Approximate Riemann solvers,Parameter vectors,and difference schemes,J.Computat.Phys.,1981,43:357~372
[6]Van Leer, B.Towards the ultimate consevative difference scheme.V.A second order sequel to Godunov’s method.J.Computat.Phys.1979,32:101~136
[7]譚維炎,淺水動力學的回顧和當代前沿問題,水科學進展,1999,10(3):296-303
[8]Monthe L.A., Benkhaldoun F.,Elmahi I.Positivity preserving finite volume Roe schemes fortransport-diffusion equations. Comput.Methods Appl.Mech.Engrg, 1999,178 :215~232;
[9] Bellos C.V., Soulis J.V., Sakkas J.G,Experimental Investigation of two-dimensional dam-break induced flows,Journal of Hydr.Res., 1992.30(1); pp47~63
Numerical Simulation of Two-Dimensional Shallow Water
Flow on lrrgular Grids
Chen Zuhua Wang Guangqian
(Dinghua University, Key Labofstory for Water and Sediment sciences of Ministry of Education,Bejing 100084)
Wang Zhishi
(The College of Science and Technologyg University of Macau)
AbstraCt:A numerical model for the solution of the two-dimensional shallow-water flow on irregular grids is described.The model,which is based on finite-volume method,adopted the Roe’sapproximate Riemann solver to deal with the advection termss in the shallow-water equations.Abilinear approximation for the topography in a discrete cell is introduced to preclude the restrictions on the Roe’s scheme to bed slope.And a modified MUSCL technique is combined to obtain an increased accuracy instead of unilateral difference method,the least square method is used to find the gradient of the primitive variables so that irregular grids can be used.The results of several examples show that the model is capable of treating discontinuities and flow transients, and is of good accuracy as well as performance for different applications.
Key words:Shallow-Water Equations,Finite-Volume Method,Roe’s scheme,Tidal Flow,The Surrounding waters of Macau
相關推薦
論文搜索
月熱點論文
論文投稿
很多時候您的文章總是無緣變成鉛字。研究做到關鍵時,試驗有了起色時,是不是想和同行探討一下,工作中有了心得,您是不是很想與人分享,那么不要只是默默工作了,寫下來吧!投稿時,請以附件形式發至 paper@h2o-china.com ,請注明論文投稿。一旦采用,我們會為您增加100枚金幣。








