劉毅,陳吉寧,杜鵬飛(清華大學環境科學與工程系環境模擬與污染控制國家重點聯合實驗室,北京　
100084 ,E-mail :jchen1 @mail. tsinghua. edu. cn)

摘要:在對水文模型實例的參數不確定性分析基礎上,分別采用傳統靈敏度分析方法、HSY算法、線性回歸等方法對模型參數特性進行了識別與比較研究. 結果表明參數優化算法與傳統靈敏度分析方法不能解釋模型結構復雜性特征,采用不確定性分析方法對環境模型參數進行識別提供了深入分析與理解模型系統的有效途徑.
關鍵詞:參數優化;不確定性;模型結構;參數識別;靈敏度;HSY算法
中圖分類號:X11 　文獻標識碼:A 　文章編號:025023301 (2002) 0620520006
基金項目:高等學校優秀青年教師教學科研獎勵計劃資助項目
作者簡介:劉毅(1975～) , 男, 博士研究生, 主要從事環境系統分析方向的研究.
收稿日期:2001210212 ;修訂日期:2002205208

　　隨著環境模型結構復雜性的急劇增長,模型參數在高維空間表現出了復雜的相關性結構并直接導致了優化后驗參數的識別問題[1 , 2 ] .因此僅僅局限于參數優化算法效率和精度等方面的研究已經不能滿足理論與實踐的需要. 相對于觀測數據和模型參數而言,基于現有科學認知體系構建的模型結構是建模過程中不確定性的根本來源[3 ] . 然而由于缺乏深入研究結構不確定性的理論基礎和有效技術手段,模型結構往往只能通過識別參數后驗統計分布規律間接地得到驗證.
　　參數不確定性依賴于模型結構,并直接導致了靈敏度問題[4 ] . 模型參數不確定性包括參數可識別性和參數靈敏度2 個基本方面. 參數不確定性分析提供了后驗地識別模型結構的可行途徑[5 , 6 ] . 本文以一個經典的水文箱式模型為實例,從優化參數的不確定性和參數識別問題出發,對復雜模型的參數靈敏度分析方法進行了比較研究.
1 　環境模型參數不確定性與識別
　　由于參數不確定性普遍存在,根據經驗估計或者觀測值優化得到的參數并不能保證模型應用的精度和預測結果的可靠性. 在追求更加高效和穩定優化算法的同時,所得到優化參數的后驗分布具有本質上的不確定性;對于復雜模型來說,甚至無法判斷優化結果是否達到了全局最優,也無法預測“最優”參數對于模型預測的影響[7 ] . 引入參數不確定性分析可以更為深刻地理解和認識到現實世界和模型系統特征之間的本質區別.
　　直接參數優化算法可以理解為在一定控制性準則約束下的空間隨機搜索過程. 算法根據新點產生器和判定準則在高維參數空間持續地進行“產生新點2判斷2接受/ 舍棄”的迭代過程,直至滿足終止準則. 為了說明參數不確定性及其識別問題,本文采用4 種直接參數優化算法進行比較分析[8 ] . 控制隨機搜索算法(CRS) 引入了幾何學中“重心”的概念,即考慮了新點產生的隨機性,又在一定程度上保證了搜索的整體性. 復合形混合演化算法( SCE- UA) 是將生物自然演化過程引入到數值計算中,模擬了生物進化的過程,提高了計算效率和全局搜索整體最優的能力. 模擬退火算法(SA) 則假設優化問題的解及其目標函數分別與固體物質的微觀狀態及其能量所對應,采用隨機方法模擬固體穩定“退火”的過程. 退火單純形算法(AS) 綜合了下山單純形方法和模擬退火法2 種優化算法,更加充分地利用了單純形的形變信息,從而提高了計算效率和算法穩定性.
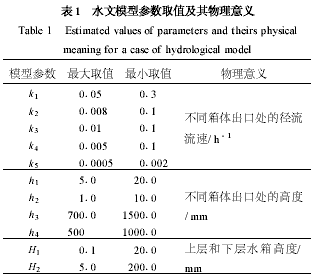
　　隨著環境模型的不斷開發和廣泛應用,環境模型的種類和數量日益豐富,模型本身所表現出的結構特征也日趨復雜. 本研究僅以一個兩箱式水文模型為例[8 ] ,表1 給出了模型中11個參數的先驗取值范圍及其物理意義.
　　　　　　　　　　　　　

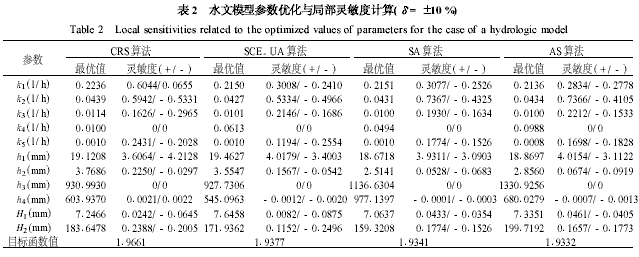
　　優化算法的基本思想認為在特定模型結構下只有唯一一組最佳參數與之對應. 然而由于模型結構復雜性與輸入數據的不確定性,優化算法通常不能尋優到環境模型的唯一真值,并且也無法判斷算法是否達到全局最優. 這是導致優化參數不確定性的根本原因. 根據4 種直接優化算法得到的優化參數結果可知,在目標函數值無顯著性差異的條件下( max δ <118 %) , “最佳”估計參數之間具有較大差異(見表2) . 由于本文采用的水文模型輸入數據序列非常完整,可以忽略其不確定性,并且幾種優化算法也是當前最為穩定和可靠的全局搜索算法[8 ] ,因此上述優化結果直接證實了優化算法不能為深入研究復雜環境模型提供有效途徑.
　　進一步研究表明,不同算法尋優進程中的參數收斂軌跡也具有較大差異[8 ] . 以CRS 算法運用于水文模型為例,圖1 是500 個最佳優化參數樣本點分布圖,其中菱形符號代表最佳的10 個參數值分布(采樣總數n = 20000) ,虛線對應于最佳目標函數值.
　　　　　　　　　　　　　　　　
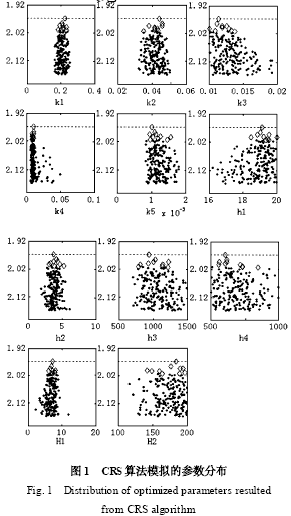
　　可以由圖直觀地看到最佳10 組參數對應的目標函數值沒有顯著區別,但這10 組參數值并沒有非常一致地收斂到“最佳”參數估計值.這種優化結果通常稱為優化參數的等效性或可置換性[7 , 9 ] . 優化參數可置換性的產生是由于模型參數在高維空間具有的復雜相關性,是模型結構復雜性和參數不確定性的集中體現. 這種與優化算法結構設計、新點產生器、空間搜索方法和接受/ 舍棄判定準則等高度相關的后驗參數空間分布上的差異性,是導致優化算法不能解釋模型結構及其所產生的參數不確定性的主要原因.
2 　環境模型的參數靈敏度
　　如前所述,優化方法不能解釋模型結構復雜性與參數不確定性,由此產生了對于模型參數的識別問題. 參數識別很重要的一個方面就是研究參數變化所引起的模型響應,即參數靈敏度問題[5 , 9 ] . 研究參數靈敏性有助于深入理解并改進模型結構的穩定性.
　　傳統參數靈敏度分析方法是在某個參數最佳估計值附近給定一個人工干擾,并計算參數在這一很小范圍內產生波動所導致模型輸出的變化率,即擾動分析方法. 從表2 的計算結果中可以得出基于4 種直接優化算法最佳參數估計值的靈敏度數值(δ= ±10 %) 具有較大差異,其結果強烈依賴于優化算法的選擇.
　　　　　
　　如前所述,由于優化算法自身結構設計決定了最佳參數估計值并得到具有特定收斂特征的參數樣本,因此基于“最佳”估計參數值的靈敏度分析不能完整地描述模型參數的空間分布形態;另一方面更為本質的是,由模型結構復雜性導致的參數相關性要求在靈敏度分析過程中必須考慮參數之間的相互影響,而不是僅靠變動某一個參數得到模型響應. 考慮到模型參數之間的高度相關性,現代環境系統研究在不確定性分析思想框架下提出了更為有效的參數靈敏度分析方法, 即區域靈敏度分析方法( Regional Sensitivity) [1 , 3 ] . 與傳統分析方法不同,區域靈敏度分析拋棄了“尋優”思想,承認參數空間分布的復雜性與相關性,是一個對模型結構在一定準則下對隨機參數大樣本發生響應的統計分析過程. 本文采用線性回歸和HSY 2 種區域靈敏度方法.
　　線性回歸方法是通過隨機采樣產生參數樣本序列,計算每個樣本對應的模型響應,然后進行線性回歸(LR) , 建立如下形式的線性模 型[6 ] :
　　　　　　　　
　　(1) 式中,βi 為對應于參數pi 的線性回歸模型系數,表征了參數pi 對模型響應y 的貢獻率(權重) ,即為基于線性回歸方法得到的參數pi的絕對靈敏度. 由于模型參數量綱不同,通常采用(2) 式計算參數相對靈敏度βi( s) , 其中σpi和σy 分別表示參數樣本和模型輸出的方差:
　　　　　　　　　　
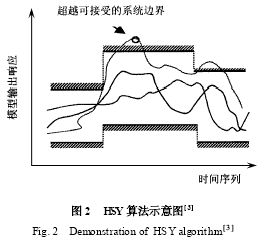
　　HSY算法用于區域靈敏度分析是基于模型某種形式的判定準則,通過隨機采樣過程產生2組參數,并根據統計檢驗方法計算參數靈敏度[3 ] . 這里的某一準則是根據已有經驗、數據或是在一定置信區間下的模擬準則,用來判斷隨機采樣的參數樣本是否被接受,體現了不確定性分析中不承認“最優”的基本思想. 可接受與不可接受2 組參數樣本共同表征了模型本質特征[1 , 5 ] .　　本文中采用(3) 式定義可接受的系統行為:Yobv[1 - αβ( n) ] ≤ Ysim ≤ Yobv[1 +αβ( n) ](3)
　　式中, n 是模型優化結果與觀測值之間的誤差向量,δ( n) 是n 維向量的樣本方差,α表示可接受系統偏差的倍數. Yobv和Ysim分別表示觀測值和模型輸出值. 這樣就形成了一個系統輸出的控制“廊道”,凡是超出這個廊道邊界的樣本,都認為是不可接受的采樣(見圖2) .
　　　　　　　　　　　　　　
　　兩樣本非參數假設檢驗的方法有χ22擬合優度檢驗, K2S 檢驗,秩檢驗,游程檢驗等,不同方法對靈敏度計算結果會產生一定影響[10 ] . 本文采用K2S 檢驗方法[1 , 5 , 10 ] . K2S 檢驗數值越大,說明可接受參數的概率分布與不可接受參數的概率分布之間的差別越大,從而參數靈敏性越大,具有明確物理意義的參數也越容易被識別. 當涉及到大樣本采樣過程時,可以采用下面的準則來判斷參數靈敏度分析算法是否達到收斂[1 ] : ①重復采樣過程,樣本均值和方差不發生變化; ②重復采用過程,模型參數的靈敏度排序不發生變化.
　　　　　
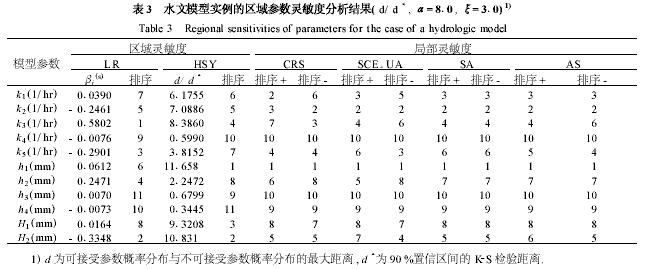
　　表３給出了采用LR 與HSY算法得到水文模型實例中的11 個參數的區域靈敏度數值及排序,作為比較同時列出了參數的局部靈敏度排序. 由于HSY算法考慮了模型結構導致的參數相關性,并且采用完全隨機采樣方法,因此其區域靈敏度分析結果具有可靠性. 而LR 算法是在整個參數可能空間上采樣,參數靈敏度中不加區分地包含了可接受與不可接受參數的特征信息;另外,盡管算法也采用了在整個參數空間上的隨機過程,但是從建立參數與模型響應之間的線性模型中得到的參數靈敏度又不可避免地抵消了模型結構自身復雜性的影響,因此其靈敏度結果是不可靠的.
　　盡管局部靈敏度數值之間存在較大差異,但某些參數的局部靈敏度排序卻出現一定程度上的一致性,例如局部最靈敏參數均為h1 . 如前所述,由于僅考慮了單一參數在“最優點”附近沿特定方向變化所引起的模型輸出響應,參數局部靈敏度不能反映出模型結構特征與參數相關性. 而HSY算法提出將參數劃分為系統可接受與不可接受樣本的思想,從根本上避免了傳統“尋優”思想帶來的模型結構和參數不確定性分析中的困惑,并通過計算2 參數樣本之間的統計距離,得到了包含參數空間分布特征整體的區域靈敏度,為優化模型結構和改進模型穩定性提供了有力的分析基礎和技術支持.
　　以部分參數為例,圖3 進一步給出了HSY算法可接受參數的最佳500 個估計值與4 種優化算法的最佳估計參數的空間分布比較. 取代唯一“最優”的參數估計值,HSY 算法以降低計算效率為代價保證了參數空間搜索的整體性,避免了優化算法定向搜索對參數特性的片面理解;并以降低計算精度為代價得到的系統可接受的參數空間,對應著可接受的模型輸出,其意義在于定量地給出參數的可識別性和模型預測結果的可靠性. 特別是在模型應用于情景分析中,傳統方法只能根據參數局部靈敏度絕對數值大小來計算未來各種可能情景下的模型響應,由于實際環境系統復雜性和參數之間的實際相關性,優化算法并不能保證模型預測的可靠性. 而采用區域靈敏度方法得到的可接受參數樣本,定量地給出了可接受模型輸出的參數空間分布,從而保證了模型整體上的預測可靠性. 正如有學者指出,與其面對沒有可靠性的優化算法,不如接受一個更為合理的不確定性[3 ] .
　　　　　　　　　　　　　　　　
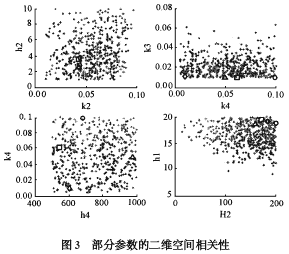
　　　　　　　　　　　(菱形、正方形、三角形與圓形分別表示CRS、SCE - UA、SA 和AS 算
　　　　　　　　　　　法的最佳參數估計值,空間點為HSY算法可接受參數的最佳500 個估計值)
　　進一步地,采用K2S 統計檢驗方法所得到的區域靈敏度數值表征了參數可識別性,其為今后模型結構不確定性研究以及模型結構的簡化和改進提供了科學分析依據[5 ] .
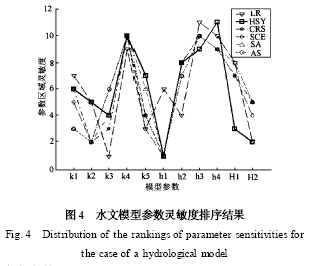
　　圖4 是基于各種區域靈敏度分析方法的參數靈敏度排序分布圖. 基于前文分析,認為只有HSY算法得到的參數靈敏度是無偏的. 無論是參數優化還是參數靈敏度分析,優化算法都不能很好地解釋環境模型復雜性和參數識別問題. 基于不確定性分析思想的HSY算法提供了識別復雜模型參數和深入理解模型結構的有效方法.
　　　　　　　　　　　　　
參考文獻:
1 　Chen J . The Modeling and Control of activated sludeg process : Towards a systematic framework. Ph. D. thesis. Imperial College , London , Engl. , U. K. 1993. 54～94.
2 　Chen J , Wheater H S. Identification and uncertainty analysis　of soil water retention models using lysimeter data. Water　Resources Research , 1999 , 35 (8) : 2401～2414.
3 　Beck M B. Water quality modeling : A review of the analysis　of uncertainty. Water Resources Research , 1987 , 23 ( 8) :1393～1442.
4 　Spear R C , Grieb T M , Shang N. Parameter uncertainty and　interaction in complex environmental models. Water Resources Research , 1994 , 30 (11) : 3159～3169.
5 　Chen J , Beck M B. Quanlity Assurance of Multi2Media　Model for Predictive Screening Tasks. USEPA , Report .1998.
6 　Klepper O. Multivariate aspects of model uncertainty analysis : Subjective calibration of incorrect models. Report . National Institute of Public Health and Environmental Protection , The Netherlands. 1999.
7 　Aalderink R H , Jovin J . Identification of the parameters describing primary production from continuous oxygen signals.　Water Science and Technology , 1997 , 36 (5) : 43～51.
8 　劉毅, 陳吉寧, 杜鵬飛. 環境模型參數優化方法的比較研究. 環境科學, 2002 , 23 (2) : 1～6.
9 　Beven K. Prophecy , reality and uncertainty in distributed　hydrological modeling. Advances in Water Resources , 1993 ,16 : 41～51.
10 　Reckhow K H , Clements J T , Dodd R C. Statistical evaluation of mechanistic water2quality models. Journal of Environmental. Engineering , 1990 , 116 (2) : 250～268.