觀測誤差對非線性環境模型參數識別的影響
文章編號:025322468(2003) 0620781205 中圖分類號:X32 文獻標識碼:A
杜鵬飛,鄧義祥1 ,陳吉寧 (清華大學環境科學與工程系,北京 100084)
摘要:采用SCE-UA 方法和RSA 方法,比較了在不同的觀測誤差條件下,優化方法和不確定性分析方法對于非線性模型參數識別的影響. 分析表明,RSA 方法是在具有觀測誤差的數據條件下進行參數識別的一種有效手段. 同時,通過比較分析,發現RSA 方法預測的濃度平均值和概率最大值與“真實值”并不完全一致. 因此,在使用RSA 方法時,應該充分考慮預測區間,以降低決策風險.
關鍵詞:觀測誤差;不確定性分析;SCE-UA;RSA
Effects of observation errors on parameter identif ication of a nonlinear environmental model
DU Pengfei ,DENG Yixiang ,CHEN Jining(Department of Environmental Sciences and Engineering Tsinghua University ,Beijing 100084)
Abstract :Parameter identification is a crucial procedure for model application. Observation errors are widely present in environmental data. Thispaper focused on the effects of observation errors on parameter identification of nonlinear environmental models. It specifically compared the identification results by the optimization and uncertainty analysis approaches , taking the SCE-UA and RSA methods as representatives respectively. It was found that the RSA was an effective approach to reduce the impacts of observation errors. It was also showed that the idntified average values or the statistically most likely values of the RSA were often not in consistence with the“true values”. It is there fore suggested that the intervals be considered as identified parameter uncertainty so as to reduce the decision2making risks.
Keywords :observation errors ; uncertainty analysis ; environmental model ; SCE-UA; RSA
作者簡介:杜鵬飛(1970 —) ,男,副教授E2mail :dupf @tsinghua. edu. cn
數學模型是環境規劃與管理的重要手段,參數是數學模型必不可少的組成部分. 一般情況下,數學模型的參數必須通過識別加以確定. 因此,參數識別是數學模型應用的重要步驟. 然而,由于環境系統的復雜性和環境監測條件的相對滯后,人們可以獲得的數據往往十分有限,并且不可避免地存在著觀測誤差,給數學模型的參數識別帶來了嚴重的影響.
優化方法是傳統的參數識別技術,在環境領域以及其它領域都有比較廣泛的應用. 優化技術的研究成果不斷涌現,由Duan 等人提出的SCE-UA 方法是比較公認的具有較高效率的優化方法之一. RSA 方法是由Hornberger 和Spear 等人提出,它是基于隨機采樣的不確定性分析方法. 本文將采用上述2 種方法研究觀測誤差對非線性環境模型參數識別的影響.
1 模型描述
考慮一個簡單的子過程方程,即污染物衰減模型:
d C/d t = - k′C (1)
式中, C 為污染物的濃度(mg/L) , k′為衰減系數(1/d) , t 為時間(d) .
這里假設k′不是常數,而與污染物濃度有關:
k′= kC/( C + M) (2)
式中, k 是系數(1/d) ,M 是限制因子(mg/L) .
根據式(2) ,當C m M 時, k′近似為常數;當C n M 時,則k′近似與C 成正比.
聯立(1) (2) 兩式: d C/d t = - kC2/( C + M) (3)
積分可得: - ln C + M/C = kt - ln C0 + M/C0 (4)
其中, C0 為初始時刻污染物的濃度(mg/L) .
注意到式(4) 中C 是t 的單調函數,因此在k 、M 和C0 已知的情況下, C 是可唯一確定的.因此記C 為t 的函數:
C = C( C0 , k ,M , t) (5)
選擇該模型作為研究對象,主要考慮到以下幾個方面的因素:首先,它是許多環境模型的組成部分,在實際中有廣泛的應用;其次,模型是動態和非線性的,參數之間具有較強的相互作用;最后,模型的結構比較簡單,參數之間的關系容易把握.
2 數據序列的產生
本文采用合成的“觀測”數據進行研究,即在已知參數值的情況下采用式(4) ,產生“真實值”時間序列,然后加上隨機撓動以模擬觀測誤差,得到“觀測值”時間序列,然后利用這些數據進行模型的識別和驗證. 這樣做的目的,是為了使系統的真實情況在掌握之中,同時模型沒有結構上的誤差,參數估計的所有的誤差僅來源于初值和觀測系列. 這使得有可能在排除結構誤差的情況下,單獨研究觀測誤差對于參數識別的影響. 合成數據方法在許多模型分析中有廣泛的使用[1 ] . 為簡潔起見,在不引起混淆的情況下,不再對“觀測值”和“真實值”加上引號.
令C0 = 20 mg/L , k = 0.2/d ,M = 10 mg/L ,由于方程(4) 是一個非線性方程,因此對于給定的時刻t ,采用牛頓方法解非線性方程求出C 值[2 ] ,再加上均值為0、標準方差為1 m/g 的隨機撓動,即撓動項為: ξ~ N (0 ,1) (6)
觀測值C′為: C′(t) = C( t) + ξ (7)
顯然,觀測誤差滿足獨立、正態和同方差的性質.
3 目標函數
由于具有多個時刻的采樣值,因此必須將多目標轉化為單目標. 考慮到上述觀測誤差是正態的獨立同分布,此時最大似然方法與最小二乘法是等價的,即目標函數為模擬值與實測值差的平方和. 大量的經驗表明,如果觀測誤差滿足上述關系,則最小二乘法目標函數是最優的目標函數. 由于模型沒有結構誤差,本文不再對方法進行相關性分析.
由于C0 的特殊性,這里考慮將C0 作為參數和不作為參數2 種方案. 不識別C0 時,參數取值空間為Ω = { ( k ,M) | 0 ≤k ≤2 ,0 ≤M ≤100} ;識別C0 時,參數取值空間為Ω = { ( k , M ,C0 ) | 0 ≤k ≤2 ,0 ≤M ≤100 ,15 ≤C0 ≤30}.
4 優化方法的識別與分析
4.1 SCE-UA 方法
優化方法是傳統的參數識別技術之一,它的形式很多,收斂速度各有不同,但本質是一樣的[3 ,4 ] . 本文采用SCE-UA 優化方法.
SCE方法是Duan 等人于1992 年在吸收了控制隨機搜索方法和遺傳算法的基礎上提出 的[5 ] ,1993 年對其進行了修正,稱為SCE-UA 方法[6 ,7 ] . SCE-UA 方法在水文學模型中得到了廣泛應用,是到目前為止對于非線性復雜模型采用隨機搜索方法尋找最優值最為成功的方法之一[5 —8 ] . SCE 方法的主要步驟為:
步驟0 初始化. 選擇p ≥1 和m ≥n + 1 ,這里p 是復雜形的個數, m 是每一個復雜形的點數,計算樣本數s = p ×m.
步驟1 產生樣本. 在可行空間Ω< Rn 采取s 個點x1 、x2 、.、xs . 計算在點xi 處的函數值f i . 在缺少前驗信息的條件下,采用均勻采樣分布.
步驟2 對點進行排序. 將s 個點以升序進行排列,將它們存貯到數組中: D = { xi , f i , i =1 , ., s} ,因此i = 1 代表了目標最小的函數點.
步驟3 復雜形劃分. 將D 劃分為p 個復雜形A1 , .,Ap ,每一個包括m 個點,以使:
![]()
步驟4 根據競爭復雜形演化算法對每一個復雜形進行演化.
步驟5 混合復雜形. 將A1 , .,Ap 替代到D 中,以使D = { Ak , k = 1 , ., p} ,對D 按目標函數的升序進行排列.
步驟6 檢查收斂性. 如果滿足收斂的標準,則結束搜索,否則回到步驟3.
有關SCE-UE 方法更為詳細的介紹見參考文獻.
4.2 初值不作為參數
采用真實序列進行參數識別,識別的結果為k = 0120 ,M = 9198 ,基本上等于模型的真實參數,說明在沒有觀測誤差的條件下,SCE-UA 方法能夠有效的識別系統的真值. 但如果采用觀測值序列,則識別的結果分別為k = 1 , M = 8116 ,盡管模擬的結果尚可,最大相對誤差不超過10 %(見圖1 (a) ) ,但參數識別結果與真實值的誤差高達400 %和716 %.
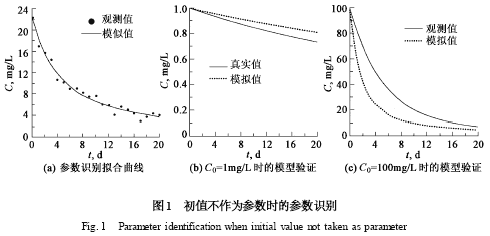
采用C0 = 1 mg/L 和100 mg/L 的系統狀態進行模型驗證,則最大相對誤差分別為1016 %和5418 % ,見圖1 (b) 和圖1 (c) . 可見,當模型進行外推時,誤差將顯著增大.
4.3 初值作為參數
當k 和M 確定以后,只要C0 確定,模擬時間序列就唯一確定了. 因此, C0 既是觀測值,也具有參數的特點. 因此可將初值也作為未知參數進行識別. 采用SCE-UA 方法進行搜索,3 個參數的識別結果分別為: k = 0126 ,M = 1511 , C0 = 2011 ,誤差分別為3015 %、5017 %和0125 %. 最優參數的擬合曲線與觀測的對比見圖2 (a) .
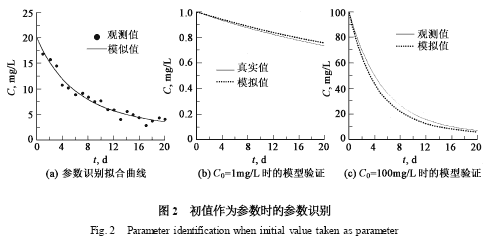
將k 和M 的識別結果代入到C0 = 1 mg/L 和100 mg/L 進行模型驗證,見圖2 (b) 和圖2 (c) .與不將初值作為參數進行識別相比,模型識別精度的改進非常明顯. 對C0 = 1 mg/L 和100 mg/L的系統狀態進行檢驗,則最大相對誤差分別為3110 %和19192 %.
5 RSA 方法的識別與分析
5.1 RSA 方法
20 世紀70 年代末、80 年代初,由于認識到模型識別的困難,Hornberger 和Spear 將過于強硬的優化條件弱化,即將其轉化為一些可以用定量或定性的語言描述的條件來決定參數的取舍,從而在一定程度上克服了采用優化方法進行參數識別而帶來的不確定性問題,這就是RSA方法. RSA 方法是基于行為和非行為的二元劃分進行參數識別的,換句話說,給定一組參數,如果系統的模擬行為滿足事先設定的條件,那么這組參數就是可接受的,否則是不可接受的. 該方法的主要步驟如下:1.確定參數的初始分布F(θ) . 如果對參數的分布特性沒有比較確切的了解,可假設參數在取值區間上均勻分布. 2.根據模擬值和觀測值的對比,確定行為參數( B)和非行為參數( NB) 的劃分準則. RSA 方法對行為參數的劃分準則非常靈活. 這提高了RSA 方法的適用范圍. 3.從參數的初始分布隨機采樣,取得一組參數,帶入模型進行模擬. 如果模擬的結果是可以接受的,那么認為這組參數是行為參數,是可以接受的;否則是非行為參數,是不可以接受的. 4.重復步驟2 和3 ,直到取得足夠的樣本數為止.
在參數空間隨機采樣1 萬次,取對應目標函數最小的5 %參數為可接受參數. 為提高采樣的效率,采用Latin Hypercube 方法[9 ,10 ] 替代傳統的Monte Carlo 采樣.
5.2 識別結果
從4.2 節和4.3 節的討論可以看出,將初值作為參數能夠更好地進行系統識別,因此RSA方法只考慮將初值作為參數的情況.
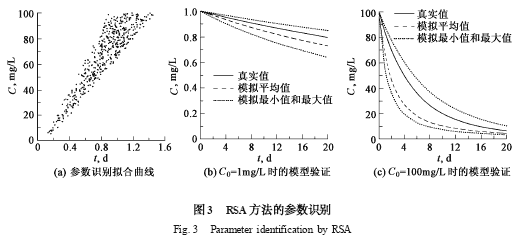
RSA 方法的模型識別結果見圖3 (a) . 由于采用了可接受行為的定義,所獲得的不再是單一的參數,而是由大量可行參數所組成的集合,其分布具有明顯的區域性特點.
當C0 = 1 mg/L 和100 mg/L 時的模型驗證見圖3 (b) 和圖3 (c) . 可以看出,各時刻物質濃度值的預測區間覆蓋了真實值,從而使模型能充分地估計預測結果的風險. 但是,與優化方法相比,RSA 方法在一定程度上犧牲了模擬精度以換取可靠性,這體現了在參數識別過程中估計精度和可靠性之間的矛盾,對其仍然需要進一步的研究.
從圖3 (b) 和圖3 (c) 可看出,RSA 方法預測的濃度平均值與真實值存在一定的偏差. 因此,在應用RSA 方法時,使用均值或概率最大值仍具有潛在的風險,應充分考慮模型預測結果的范圍,以降低決策風險.
6 結論
本文采用SCE-UA 方法和RSA 方法,研究了觀測誤差對模型參數識別和預測的影響. 為避免模型結構誤差的影響,引入了合成數據方法. 在具有觀測誤差的情況下,采用優化方法不能很好地識別模型的參數. 在本例中優化方法的分析表明,將初值作為參數進行識別,可提高系統的可識別性. 采用RSA 方法,參數識別結果不再是單一值,而是由大量可行參數所形成的集合. RSA 在一定程度上克服了觀測誤差帶來的預測風險,但模型預測的精度也因此而降低. 這體現了參數識別時預測精度和可靠性之間的固有矛盾.
參考文獻:
[ 1 ] Ratto M,Tarantola S ,Saltelli A. Sensitivity analysis in model calibration :GSA2GLUE approach[J ] . Computer Physics Communication ,2001 ,136 :212 —224
[ 2 ] 徐士良. Fortran 算法常用算法程序集[M] . 北京:清華大學出版社,1995. 123 —125
[ 3 ] 弄文訓,謝金星. 現代優化計算方法[M] . 北京:清華大學出版社,2001. 1 —245
[ 4 ] 劉 毅,陳吉寧,杜鵬飛. 環境模型參數優化方法的比較研究[J ] . 環境科學,2002 ,23(2) :1 —6
[ 5 ] Qingyun Duan ,Soroosh Sorooshian ,Vijai Gupta. Effective and efficient global optimization for conceptual rainfall2runoff models[J ] .Wat Res Res ,1992 ,28 (4) :1015 —1031
[ 6 ] Soroosh Sorooshian ,Qingyun Duan ,Vijai Kumar Gupta. Calibration of rainfall2runoff models :application of global optimization to the sacramento soil moisture accounting model [J ] .Wat Res Res ,1993 ,29 (4) :1185 —1197
[ 7 ] Duan D Y,Gupta V K,Sorooshian S. Shuffled comples evolution approach for effective and efficient global minimization[J ] . Journal of Optimization Theory and Applications ,1993 ,76 (3) :501 —520
[ 8 ] Qingyun Duan ,Soroosh Sorooshian ,Vijai K Gupta. Optimal use of the SCE-UA global optimization method for calibration watershed model [J ] . Journal of Hydrology ,1994 ,158 :265 —284
[ 9 ] Jining Chen. Modeling and control of the activated sludge process :towards a systematic framework[D] . The University of London , 1993. 130 —165
[10 ] 鄧義祥,陳吉寧,杜鵬飛. HSY算法在水質模型參數識別中的應用[J ] . 上海環境科學,2002 ,21(8) :497 —500
論文搜索
發表時間 至
月熱點論文
論文投稿
很多時候您的文章總是無緣變成鉛字。研究做到關鍵時,試驗有了起色時,是不是想和同行探討一下,工作中有了心得,您是不是很想與人分享,那么不要只是默默工作了,寫下來吧!投稿時,請以附件形式發至 paper@h2o-china.com ,請注明論文投稿。一旦采用,我們會為您增加100枚金幣。








