張雅君, 劉全勝
(北京建筑工程學院城市建設工程系，北京100044)

　　摘 要：從灰色模型的特點與需水量本身的變化規律出發，揭示了GM(1,1)模型的應用條件及其在需水量預測中的應用范圍，以東京都需水量為例進行了驗證，并對北京市需水量進行了灰色預測。?
　　關鍵詞：需水量；灰色模型；預測?
　　中圖分類號：TU991.31
　　文獻標識碼：C
　　文章編號：1000-4602(2002)03-0079-03

　　灰色系統理論認為，盡管客觀事物或系統表象復雜、數據離亂，但它總是有整體功能和有序的，具有某種內在規律，關鍵在于怎樣用適當的方法去挖掘和利用它［1］。灰色預測模型(GM)通過對原始數據進行生成處理，使其呈指數趨勢變化，建立指數微分方程，最終得到預測模型。?
　　GM的一般表達式為GM(h,n)，即對n個變量用h階方程表示。基于灰色系統的特點，大多數預測模型采用GM(1,1)及其改進模型。
　　由于初始時序列是否滿足非負的齊次指數變化規律是能否用GM建模的關鍵，因此建模條件應是初始時序列滿足指數變化規律。從數學角度看，非負的指數序列實質上就是相對增長率恒定的序列，所以判斷一個序列是否適用于GM建模的依據也應從序列的相對增長率入手，基于此提出一種新的相對增長率判定準則。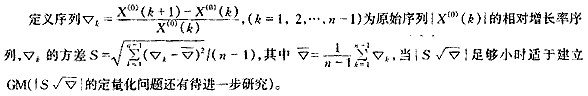 　

1 　理論依據及應用條件

　　灰色模型是一個指數模型，這也就決定了它應該用在按指數變化的系統。所以，探討一個系統是否可用灰色預測的方法，實質上是討論該系統是否按指數規律變化(同樣可用判定)。?
　　在其他因素不變的條件下，城市需水量增長與人口增長呈線性關系，而人口的增長方式在一定時期內符合指數增長規律^［2］。此外，經濟的發展在一定時期內表現為等相對增長率的指數增長規律(如目前我國的經濟增長率維持在7%～8%左右)。在不受水資源短缺制約的條件下，經濟的增長必然帶動需水量的增長。而用水系統本質上并沒有一階正反饋系統特性，需水量增長速率與該時期的用水量并沒有邏輯上的關系。但是，基于需水量與人口、經濟之間的密切關系，在需水量增長不受水資源約束時，人口、經濟的指數增長特性將傳遞給需水量，此階段用GM建模可得到較好的預測結果。?
　　因水資源短缺，使得工業和生活用水受到約束，各國政府都采取了節水措施，此時用水量的增長不再隨人口、經濟等比例增長。一方面經濟、人口的增長使需水量呈上升趨勢；另一方面由于用水政策、結構調整、工藝改革等諸多原因使需水量出現下降的趨勢。所以，此時的用水量呈波動性上升趨勢(值偏高)，不宜用GM建模預測。?
　　未來某些國家可能出現人口下降趨勢(特別是中國、日本等人口密度高的國家)，而且在以節約資源為特點的可持續發展模式中，產業結構的調整、科技的進步也勢必引起需水量的下降。需水量的負增長在這一時期內也以等相對增長率的指數方式減少，因此用GM建模也能得到較好的預測結果。?
　　以日本東京都需水量情況為例，GM模型的應用條件得到了很好的驗證。東京都水道局負擔23個區及多摩地區的供水，東京都1960年—1999年的人口增長情況如圖1所示。其中，20世紀60年代初到70年代中呈現出快速增長的勢頭，這一時期經濟增長率相對較高，人口、經濟的指數增長特性傳遞給需水量，因此它呈現出指數增長趨勢，用GM建模可得到較好的預測結果。

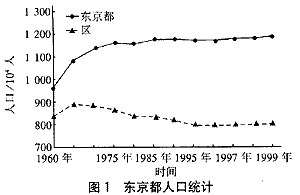
　　以1978年—1986年的用水量數據建立灰色模型，結果見表1。?

表1 東京都1978年—1986年用水量數據擬合結果 年份 實際值(10⁴m³/a) 擬合值(104m3/a) 相對誤差(%) 平均相對誤差(%) C值 1978 1776 1776.0 0.00 0.90 0.5719 1979 1728 1706.3 1.25 1980 1665 1704.5 -2.37 1981 1694 1702.6 -0.51 1982 1706 1700.8 0.31 1983 1728 1698.9 1.68 1984 1710 1697.1 0.75 1985 1690 1695.3 -0.31 1986 1678 1693.4 -0.92 　注： 實際值＞擬合值時，相對誤差為正值；實際值＜擬合值時，相對誤差為負值。

　　從表1的C值結果看，也證實了用水量波動上升期間不宜采用GM建模。由人口緩慢增長、傳統家庭形式的變遷、經濟緩慢增長等現象推測，未來較長時期內東京都需水量增加緩慢，其預測模型如下：

　　

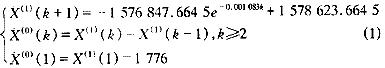
2 　北京市需水量的灰色預測

　　以北京市1989年—1999年的用水量數據(見表2)建立GM模型并進行預測。

表2 北京市用水量數據　10⁴m³/a? 年份 工業用水量 生活用水量 總用水量 1989 454105.3 51428.7 96834 1990 40939.8 52852.8 93792.6 1991 38327 56619.5 94946.5 1992 41575 58376.6 99951.6 1993 38251.7 62571.9 100823.6 1994 41431.2 67295.2 108726.4 1995 39437.3 70540.5 109977.8 1996 39824 69860.5 109684.5 1997 41622.1 75573.5 117195.6 1998 35644.8 78731.9 114376.7 1999 37354.7 82715.5 120070.2

　　工業、生活、總用水量的相對增長率k及其方差S的計算結果如表3所示。

表3 ?k及S計算結果 項目 工業用水量的k 生活用水量的k 總用水量的k 1 -0.098 0.028 -0.031 2 -0.064 0.071 0.012 3 -0.085 0.031 0.053 4 -0.080 0.072 0.009 5 0.083 0.075 0.078 6 -0.048 0.048 0.012 7 0.010 -0.010 -0.003 8 0.045 0.082 0.068 9 -0.145 0.042 -0.024 10 0.048 0.051 0.050 -0.0164 0.0490 0.0224 s 0.0770 0.0266 0.0359 4.70 0.54 1.604

　　工業用水量的GM(1,1)模型如下：

　　

　　生活用水量的GM(1,1)模型如下：

　　

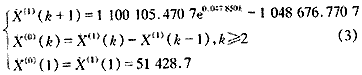
　　總用水量的GM(1,1)模型如下：

　　

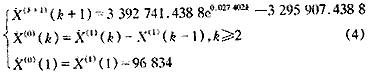
　　擬合及預測結果如表4所示。

表4 數據擬合值及2000年—2002年預測結果 項 目 工業用水量 生活用水量 總用水量 實際值(10⁴m³/a) 擬合值(10⁴m³/a) 相對誤差(%) 實際值(10⁴m³/a) 擬合值(104m3/a) 相對誤差(%) 實際值(10⁴m³/a) 擬合值(104m3/a) 相對誤差(%) 1989年 45405.3 45405.3 0.00 51428.7 51428.7 0.00 96834.0 96834.0 0.00 1990年 40939.8 40746.1 0.47 52852.8 53920.0 -2.02 93792.6 94252.9 -0.49 1991年 38327.0 40450.4 -5.54 56619.5 56562.8 0.10 94946.5 96817.1 -2.03 1992年 41575.0 40156.8 3.41 58376.6 59335.1 -1.64 99951.6 99562.4 0.40 1993年 38251.7 39865.4 -4.22 62571.9 62243.3 0.53 100823.6 102328.4 -1.49 1994年 41431.2 39576.1 4.48 67295.2 65294.1 2.97 108726.4 105171.1 3.27 1995年 39437.3 39288.9 0.38 70540.5 68494.3 2.90 109977.8 108092.9 1.71 1996年 39824.0 39003.7 2.06 69860.5 71851.5 -2.85 109684.5 111095.8 -1.29 1997年 41622.1 38720.7 6.97 75573.5 75373.2 0.27 117195.6 114182.1 2.57 1998年 35644.8 38439.7 -7.84 78731.9 79067.5 -0.43 114376.7 117354.1 -2.80 1999年 37354.7 38160.7 -2.16 82715.5 85942.9 -0.27 120070.2 120614.3 -0.45 2000年 37883.8 87008.2 123965.1 2001年 37608.8 91272.8 127409.0 2002年 37335.9 95746.4 130948.4 平均相對誤差（%） 3.412 1.271 1.500 C值 0.5066 0.0602 0.1236

　　由表3、4中數據可見，工業、生活用水量及總用水量中工業用水量的=4.7為最大(C=0.5066)，預測結果不可靠。究其原因，一方面北京市工業產業結構的調整、節水措施的加強使工業用水量呈減少趨勢；另一方面工業的高速發展使其用水仍不斷增加，因此表現出極強的波動性，不宜用灰色方法預測。生活用水量的=0.54為最小(C=0.0602)，可判定結果可靠。這是由于生活水平的提高、城市人口增長緩慢，生活用水量仍保持較為平穩的指數增長趨勢所致。總用水量在工業、生活用水雙重因素的影響下表現出一定的波動性，但用GM進行較短周期的預測可得到較好的效果(C=0.1236)，若周期過長則可靠度降低。

3 　結論

　　GM(1,1)模型本身是一個指數模型，其預測效果在很大程度上取決于原始數據的特點。用水量在某些時期內表現出一定的指數變化規律，適用于GM(1,1)模型；而在某些時期則表現出較強的波動性，不宜用GM(1,1)模型。
　　此外，一般按指數規律變化的狀態變量的增長常數隨時間變化，所以GM(1,1)模型的預測周期不宜太長，否則將帶來很大的系統誤差。

參考文獻：

　　［1］聶相田,邱林,朱普生,等.水資源可持續利用管理不確定性分析方法及應用［M］.鄭州:黃河水利出版社，1999.
　　［2］王其藩.系統動力學［M］.北京:清華大學出版社，1988.

---

　　電　　話：(010)68322517(O)?
　　E-mail:uced@mail.bicea.net.cn
　　收稿日期：2001-07-10?
　　修回日期：2001-08-08