李斌1，許仕榮1，柏光明2，李黎武1?
( 1.湖南大學土木工程學院，湖南長沙410082； 2.長沙市自來水公司，湖南長沙410015)

　　摘　要： 針對城市用水量的預測，建立了以預測方法有效度為優化指標的求解組合預測權重系數的優化模型，并對灰色—神經網絡的二元組合預測模型采用簡化方法求解。該方法應用于長沙市河西供水系統的用水量短期預測，誤差較小，能滿足實際需要。
　　關鍵詞：城市用水量；組合預測；近似最優解；灰色—神經網絡
　　中圖分類號：TU991.31
　　文獻標識碼：C
　　文章編號：1000-4602(2002)02-0066-03

　　城市用水量預測是進行城市建設規劃、輸配水系統優化調度的一項十分重要的前提工作，可分為中長期預測和短期預測。常用的預測方法有兩類：一類是因果解釋性預測方法，即假定用水量與另外幾個獨立的影響因素之間的因果關系，從而建立起預測變量與影響因素之間的關系模型，其代表性方法有多元線性回歸法、多元非線性回歸法、人工神經網絡法等；另一類為歷史數據法，它只依賴于被預測量的歷史觀測數據及觀測模式，通過序列分析找出其順序變化規律并外推出未來的值，其代表性方法有時間序列分析法、灰色預測法等。
　　然而城市用水量的變化是一個指標和影響因素繁多的復雜系統，對其系統結構及輸入和輸出的模擬、預測和調控采用單個預測模型或部分因素和指標僅能包含或體現該系統的局部，若采用多個不同的預測模型并加以適當的有效組合或多個變量的科學綜合，則可以充分地利用各種信息達到提高預測精度的目的。

1　灰色—神經網絡組合預測

　　時用水量預測采用了GM(1,1)灰色預測模型，它是只包含用水量一個變量的一階微分方程構成的模型，該模型的主要特點是所需自變量個數和歷史數據樣本個數都比較少。
　　人工神經網絡采用應用較廣泛的反向傳播BP模型，以天氣狀況、節假日情況、日最高溫度和日最低溫度作為影響因素，以時用水量作為其輸出值，故BP網絡的拓撲結構可確定為：4個輸入層神經元、6個隱含層神經元和1個輸出層神經元。
　　湖南大學謝德華的學位論文中給出了以上兩種方法的數學模型及求解方法，在此基礎上建立了兩者的組合預測模型及其求解方法。
1.1　模型的建立
　　①預測方法有效度概念?
　　設yt(t=1,2,…,N)為實際值，fit為某一預測方法的預測值，Ait為fit在時刻t的預測精度(其中N為預測數據個數)，則：
?　　　　　Ait=1-｜(y_t-f_it)/yt｜　　　　　　(1)
　　由Ait構成預測方法fit的精度序列，該序列的均值與均方差分別為：

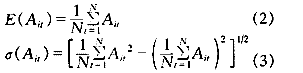
　　則預測方法fi的有效度指標定義為：
?　　　　Si=E(Ait)［1-σ(Ait)］　　　　(4)?
　　②組合預測優化模型?
　　以有效度為指標建立求解組合預測權系數k的優化模型。
　　設yt(t=1,2,…,N)為實際觀測值；fit，…，fmt為m種預測方法的預測值；ki，…，km為各預測方法的加權系數；yt=k1f1t+k2f2t+…+kmfmt為組合預測方法的預測值；At為組合預測在t時刻的預測精度，則：

　　由式(4)可知，該組合預測的有效度指標為：?
?　　　　　　　S=E(At)·［1-σ(At)］　　　(6)?
　　因此S越大，說明該組合預測方法越有效，則以式(6)為目標函數，考慮加權系數的規范性約束，可以得如下的優化模型：

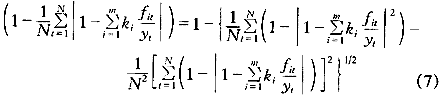
1.2　模型的近似最優解
　　模型中由于有絕對值的存在和權系數所在位置的分散，其求解十分復雜，當對城市用水量的預測用于輸配水系統的實時調度時將很不實用。因此，必須加以簡化，尋求一個近似最優解。
　　在只有兩個預測方法組合的情況下，通過數學分析，可知At、E(At)、σ(At)與組合權系數k之間存在如下幾個近似關系：
　　①組合預測精度At與組合權系數k的近似關系：
?　　　　　　　　At=kA_1t-(1-k)A_2t　　　(8)?
　　②組合預測精度序列均值E(At)與權系數k的近似關系：?
?　　　　　　　　E(At)=kE(A1t)+(1-k)E(A_2t)?　　　(9)?
　　③組合預測精度序列均方差σ(At)與權系數的近似關系為：?

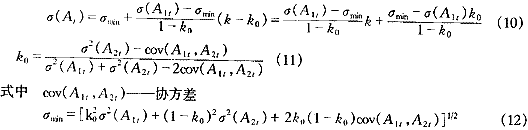
　　將式(9)、(10)代入優化模型(7)中得求解權系數近似解的簡化模型為：

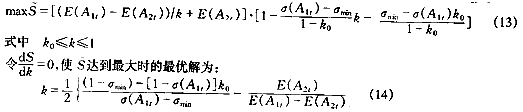
　　當由式(14)確定的k值不在［k0,1］之間時，應對其進行修正，設σ1、σ2分別為預測方法f1、f2與實際值的均方差，則有：
?　　k=k_修正=σ²/(σ1+σ²)　　　　(15)?
1.3　時用水量預測的簡要步驟
　　①用灰色GM(1,1)模型和人工神經網絡模型分別進行預測，得預測序列y1和y2；
　　②由式(2)、(3)計算E(y1)、E(y2)、σ(y1)、σ(y2) 及兩個序列的協方差cov(y1,y2)；一般情況下兩種預測方法是相互獨立的，因此cov(y1,y2)=0；
　　③由式(11)、(12)求出k0、σmin；
　　④若k0=1，則k=1，轉步驟⑤，否則轉步驟⑥；
　　⑤計算組合預測值，輸出預測值序列，結束計算；
　　⑥按式(14)、(15)求出權系數k，轉步驟⑤。

2　應用實例

　　在長沙市自來水公司863/CIMS應用示范工程的管網調度系統中，運用了灰色—神經網絡組合預測方法對河西區管網用水量進行短期預測。其中一組實測數據如表1。 表1　　實測時用水量　　　m³/h? 日期 時用水量 日期 時用水量 日期 時用水量 7月29日 5750.50 8月8日 5963.25 8月20日 5700.00 7月30日 5887.00 8月9日 5465.25 8月21日 5750.50 7月31日 5893.00 8月10日 5894.75 8月22日 5600.00 8月1日 5561.00 8月11日 5469.25 8月23日 5553.25 8月2日 5839.50 8月12日 5640.50 8月24日 5834.00 8月3日 5569.00 8月13日 5996.75 8月25日 5897.00 8月4日 5881.25 8月14日 5723.00 8月26日 5724.50 8月5日 6283.50 8月15日 5718.00 8月25日 5575.50 8月6日 5576.00 8月16日 5924.50 8月26日 5690.50 8月7日 5973.75 8月17月 5631.00 8月27日 5659.50

　　用表1中7月29日—8月12日的數據作為樣本，對8月13日—8月27日8時～9時的時用水量用灰色方法、BP神經網絡方法、灰色—神經網絡組合預測方法分別進行預測，結果見表2。 其中組合預測中灰色預測的權系數為0.667，神經網絡預測的權系數為0.333。 表2 時用水量預測結果 實際用水量(m³/h) 灰色預測 神經網絡預測 組合預測 預測值(m³/h) 誤差(%) 預測值(m³/h) 誤差(%) 預測值(m³/h) 誤差(%) 5996.75 5689.41 5.13 6100.00 -1.72 5826.10 2.84 5723.00 5777.53 -0.95 5963.00 -4.19 5839.28 -2.03 5718.00 5719.65 -0.029 6002.00 -4.97 5813.65 -1.67 5924.50 5718.10 3.48 6002.00 -1.31 5812.62 1.88 5631.00 5698.37 -1.20 5500.00 2.33 5632.33 -0.02 5700.00 5672.86 0.48 5500.00 3.51 5615.31 1.48 5750.50 5739.21 0.20 5500.00 4.35 5659.57 1.58 5600.00 5732.52 -2.37 5500.00 1.79 5655.11 -0.98 5553.25 5716.45 -2.94 5570.00 -0.29 5667.69 -2.06 5834.00 5692.11 2.43 5500.00 5.73 5628.15 3.52 5897.00 5767.27 2.20 5661.00 4.00 5731.89 2.79 5724.50 5790.34 -1.15 5793.00 -1.20 5791.23 -1.16 5575.50 5722.12 -2.63 5500.00 1.35 5648.17 -1.30 5690.50 5643.20 0.83 5500.00 3.35 5595.53 1.66 5659.50 5701.52 -0.74 5718.00 -1.04 5707.01 -0.83

　　為檢驗預測效果的好壞，按照整體評價預測方法的原則和慣例，采用以下指標來評價：?
①平均絕對誤差?

　　式中　0≤U≤1，U→0精確度高，U→1精確度低
?　　　　yi——實際值
?　　　　——預測值
?　　　　n——預測數據個數
　　評價結果見表3。 表3　預測效果評價表 預測方法 MAE MAPE U 有效度(S) 灰色預測 102.99 0.0178 0.0114 0.9688 神經網絡預測 157.73 0.0274 0.0160 0.9570 組合預測 99.58 0.0173 0.0097 0.9744

　　由表3可知，灰色—神經網絡組合預測的三項指標全部優于灰色預測和神經網絡預測，充分顯示了該方法的優勢；且表2中組合預測的單個預測值誤差也完全達到了城市供水調度所需的工程精度，表明組合預測適用于生產實際。

參考文獻：

　　 ［1］許仕榮.配水系統優化調度［J］.湖南大學學報，1998,25(6)：86-91.
［2］ 馬永開，唐小我.線性組合預測模型優化問題研究［J］.系統工程理論與實踐，1998，18(9 )：110-114.
［3］馬永開，唐小我.多目標組合預測優化模型研究［J］.統計研究，1997，(4) ：45-48.
［4］ 董景榮.一種新的基于模糊模型的非線性組合預測方法及其應用［J］.系統工程理論與實踐，2000，20(5)：109-144.
［5］ 王明濤.確定組合預測權系數最優近似解的方法研究［J］.系統工程理論與實踐，2000，20(3)：104-109.

　　電　　話：013517314267?
　　收稿日期：2001-06-17