字典序目標規劃法在大型供水管網改、擴建工程優化決策中的應用
| 論文類型 | 技術與工程 | 發表日期 | 2001-11-01 |
| 來源 | 2001年中日水處理技術國際交流會 | ||
| 作者 | 楊曉安,邱文心,王萍 | ||
| 關鍵詞 | 字典序 目標規劃 供水管網 靈敏度 | ||
| 摘要 | 本文將字典序線性目標規劃基本模型應用于大型供水管網改、擴建優化決策,建立了大型供水管網改、擴建工程優化決策字典序線性目標規劃模型,并用字典序線性目標規劃多階段算法進行計算,編制了相應的計算程序,且根據其計算特點,編制了字典序線性目標規劃靈敏度分析程序,對所建立的模型進行靈敏度分析。計算實例表明:字典序線性目標規劃法的理論和方法非常適合大型供水管網改、擴建工程優化決策計算,結果令人滿意。所編制程序具有準確性和通用性,對生產具有科學和實際的指導意義。 | ||
楊曉安 邱文心 王萍
(武漢市自來水公司 430034)
摘 要:本文將字典序線性目標規劃基本模型應用于大型供水管網改、擴建優化決策,建立了大型供水管網改、擴建工程優化決策字典序線性目標規劃模型,并用字典序線性目標規劃多階段算法進行計算,編制了相應的計算程序,且根據其計算特點,編制了字典序線性目標規劃靈敏度分析程序,對所建立的模型進行靈敏度分析。計算實例表明:字典序線性目標規劃法的理論和方法非常適合大型供水管網改、擴建工程優化決策計算,結果令人滿意。所編制程序具有準確性和通用性,對生產具有科學和實際的指導意義。
關鍵字:字典序 目標規劃 供水管網 靈敏度
The Lexicographic Linear Goal programming is applied to the
Optimal Decision-making of the large Water Networks
Rebuliding & Enlarging project
Abstract:The basic model of the lexicographic linear Goal programming is applied to calculating the optinal decision-making of the large water networks rebuliding & enlarging project.A model used for calculating the optimal decision-making of the large water networks rebuliding & enlarging project is constructed.The lexicographic linear Goal programming mutiplestage algorithm is used to calculate. A
correlative calculating program is programmed.According to its calculating characteristics, the procedure
of the lexicographic linear Goal programming sensitivity analysis is made to analyse the constructed
model.The calculating example indicates that,the theory and the method of the lexicographic linear Goal
programming is very suitable for the calculation of the optimal decision—making of the large water networks rebuliding & enlarging project.The result proves satisfactory.The programs are precise and stable.They have scientific and practical guiding value to production.
key words:LexiGographic Goal progrmming water networks sensitivity
1 字典序線性目標規劃基本模型[1][2]
1.1字典序線性目標規劃方法的概念
字典序線性目標規劃(Lexicopraphic Linear Goal programming)簡稱LLGP是美國阿波羅計劃工程師J.P伊格尼齊奧于1976年在研究目標規劃法的基礎上提出的一種用目標偏差量有序向量衡量多目標模型目標達成度的字典序最小方法。
1.2數學模型
LLGP方法的數學模型為:
求x(x1,x2,…,xn)
使 Lexmin α={g1(η,δ),g2(η,δ),…,gk(η,δ)} (1-1-1)
s.t ∑nj=1=cI,jxj+ηi-δi=bi ,i=1,2,…,m (1-1-2)
x,η,δ≧0 (1-1-3)
其中:x—n維決策變量;η—負偏差變量;δ—正偏差變量; gk(η,δ)—為第K個優先級別中目標偏差變量的線性系數:α—尋求字典序極小化達成系數;cI,j—是對應于第i個目標或約束中第j個變量的系數;bi—為目標或約束分端常數:(1-1-1)為LLGP問題的目標;(1-1-2)為目標的約束條件,可以有硬約束和軟約束;(1-1-3)為非負約束,即x、η與δ均為非負變量;k—為優先次序數。m—為全部目標和約束數。
1.3字典序線性目標規劃模型的求解方法:
字典序線性目標規劃模型最常用的求解方法是多階段單純形算法,它的目標行里有多個目標存在,進行單純形迭代時,按確定的優先次序分層次的解決問題,它得到多個目標滿足約束條件下的滿意解。
2 字典序線性目標規劃模型靈敏度分析方法[3]
2.1靈敏度分析
靈敏度分析是考查模型結構中,某元素變化對問題解的影響。
2.2字典序線性目標規劃靈敏度分析的三種方法:
(1) 結構性離散變化:①重捧優先級②增加新變量⑧增加變目標;
(2) 非結構性離散變化:有vh+毗k,yl+及h的離散變化:
(3) 在一個區域連續取值的參數分析:即參數線性目標規劃。
3 大型供水管網改、擴建工程優化決策字典序線性目標規劃計算模型
大型供水管網改、擴建工程優化決策問題的目標是多個的,既有總水量目標,又有各輸送管道及轉壓站輸送水量目標,還有控制費用目標,而且這些目標的重要程度是不同的:首先,須滿足總水量目標,其次是控制費用及各輸送輸送管道及轉壓站輸送水量目標,除滿足上述目標外,還須滿足在每種輸送方式下各種輸送管道及增壓站的輸送水量小于或等于該種輸送方式下的輸送水量。 下述表明:大型供水管網改、擴建工程優化決策問題,實際上是個多目標規劃問題,其約束和目標方程都是線性的,因而完全適合字典序線性目標規劃法求解條件。
3.1已知條件:
(1) 所考察的各類水量;S1,S2,……,Sp;
(2) 每種輸送方式費用單價:C11,C12,…,C1q1;…,…,…,…;
Cp1,Cp2,…,Cpqp;
(3) 各條輸送管道及各轉壓站的輸送水量;A1,A2,……,Ar
(4) 所有改.擴建管道及轉壓站項目的控制費用:W
3.2待求變量:
(1) 每類水量適宜的輸送方式輸送該類水量的量:
X11,X12,…,X1q1;…,…,…,…;xp1,xp2,…,xpqp;
(2) 每種輸送方式下換輸管道和轉壓站所輸送水量:
x111,x112,…,x11r11;…,…,…,…;xpqp1,xpqp2,…,xpqprpqp;
(3) 各種輸送方式下各種輸送管道和轉壓站的輸送水量:;
x11A1,x11A2,…,x11Ar;…,…,…,…;xpqpA1,xpqpA2,…,xpqpAr;
3.3計算模型:
3.3.1目標:
(1)每類水量各輸送方式所輸送水量之和與該類水量相等,即:
∑q1j1=1x1j1=S1;∑q2j2=1x2j2=S2;…;∑qpjp=1xpjp=Sp; (3-1-1)
(2)輸送各類水量各輸送方式管道及轉壓站改、擴建費用之和等于總控制費用:
∑q1j1=1C1j1x1j1+∑q2j2=1C2j2x2j2+…∑qpjp=1Cpjpxpjp=w; (3-1-2)
(3)輸送各類水量同一種管道求轉壓站所輸送水量應該等于該管道求轉壓站所輸送的水量:
∑q1j1=1x1j1A1+∑q2j2=1x2j2A1+…∑qpjp=1xpjpA1;…;∑q1j1=1x1j1Ar+∑q2j2=1x2j2Ar+…∑qpjp=1xpjpAr=Ar
3.3.2約束條件:
(1) 水量約束:
每種輸送方式下換輸管道和轉壓站所送水量小于等于該輸送方式所輸送的水量:
(2) 非負約束:X≧0;
3.3.3優先級:一級為各類水量目標;二級為控制費用目標;三級為各管道和轉壓站輸送水量日標;
4 大型供水管網改、擴建工程優化決策字典序線性目標規劃模型靈敏度分析
4.1某些問題的處理:
(1)考慮到四舍五入帶來的影響,為方便編程計算,特作如下規定:凡本模型靈敏度分析中間值的絕對值小于或等于0.00001的元素值均設為0.0。
(2)為方便編程計算:在本模型靈敏度分析中,用1.0e+35代替+∞,-(1.0e+35)代替-∞。
4.2單元素變化及多元素參數分析:
均針對第t個方案,在保持目前最優基的條件下,求滿足下列不等式:B-1(b+ubt*)≧0的u的 取值范圍(因篇幅所限,公式推導及結果省略).
4.3離散變化的靈敏度分析:
從單元素變化及多元素參數分析所確定的各取一u值,計算XTb*B-1(b+ubt*)及atk*=∑m+ns=1Wk,s*XTb,s*+∑mI=1uI,k*XTb,I*
其中:t—單元素變化或多元素參數分析的第t個方案;XTb,s*—問題變量中的負偏差變量值;XTb,I*—問題變量中的正偏差變量值。
5 大型供水管網改擴建工程優化決策字典序線性目標規劃模型多階段單純形算法程序框圖及靈敏度分析程序框圖[4]
5.1多階段單純形算法程序框圖

5.2靈敏度分析程序框圖
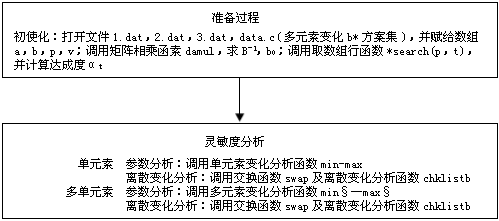
6 例計算和分析
6.1實例
1.武漢武昌地區“湖改江”工程,含東湖水廠“湖改江”和團山水廠“湖改江”,根據武昌地區供水規劃,實現東湖水廠“湖改江”須補充水量12萬噸/日,實現團山水廠“湖改江”須增加水量18萬噸/日。
2.實現東湖水廠"湖改江"有以下六種可能輸送方式:
(元/m3) 1 南湖北路轉壓站 南湖北路DN1200管 600 2 關山路轉壓站 南湖北路DN1200管 450 3 關山路轉壓站 南湖南路DN800管 300 4 關山路轉壓站 關山一路延長線DNl000管 300 5 南湖北路DNl200管 關山一路延長線DN1000管 450 6 湖邊泵站 南湖北路DN1200 600
(B)實現團山水廠“湖改江”有以下十種可能輸送方式:
序號 前輸 轉輸 改、擴建單位費用(元/m3) 1 三環路DN400管 三環路轉壓站 600 2 三環路DN400管 天京路DN300管 600 3 三環路DN400管 三環路DN100管 900 4 南湖北路轉壓站 魯巷廣場 600 5 關山路轉壓站 南湖南路 300 6 關山路轉壓站 關山路延長線DN1000管 300 7 關山路轉壓站 民院路DN400管 600 8 關山路轉壓站 天京路ON300管 900 9 湖邊泵站 環湖路DN300管 450 10 三環路轉壓站 關山一路延長線DN1000管 300
3.根據管網水力計算,各轉壓站及管道增輸水量(萬噸)情況如下:
南湖北路轉壓站:12;南湖北路DNl200管:12;湖邊泵站:3;三環路轉壓站:6;南湖南路DN800管;4.5;關山路轉壓站;7;關山一路延長線DNl000管;7:環湖路DN300;0.5;天泉路DN300:0.5;民院路DN400管:0.5;三環路DN400管:3;魯巷廣場DN800管:4。
4.根據控制費用:實現武昌地區"湖改江"管網及轉壓站改、擴建控制費用為:1.5億元。
要求選擇適宜的輸送方式并求各適宜輸送方式下各輸送管道及轉壓站的轉輸水量。
6.2本問題是一個典型的大型供水管網,改、擴建工程優化決策問題。
它須滿足總水量及單水量目標,還須滿足控制費用目標,硬目標為是總水量目標,單水量及控制費用為軟目標,因此,該問題屬字典序線性目標規劃問題,故可用本文的字典序線性目標規劃模型求解程序求解,并進行模型的靈敏度分析。
6.2.1字典序線性目標規劃分階段算法程序求解結果及分析
(1) 東湖水廠"湖改江"
(2) 團山水廠"湖改江"
序號 前輸 水量(萬噸) 轉輸 水量(萬噸) 1 三環路DN400管 0 三環路轉壓站 0 2 三環路DN400管 0 天京路DN300管 0 3 三環路DN400管 1.5 三環路DN100管 1.5 4 南湖北路轉壓站 4.0 魯巷廣場 4.0 5 關山路轉壓站 4.5 南湖南路 4.5 6 關山路轉壓站 0.5 關山路延長線DN1000管 0.5 7 關山路轉壓站 0.5 民院路DN400管 0.5 8 關山路轉壓站 0.5 天京路ON300管 0.5 9 湖邊泵站 0.5 環湖路DN300管 0.5 10 三環路轉壓站 6 關山一路延長線DN1000管 6 由上表可知:東湖水廠"湖改江"中改、擴建單位費較低的兩種輸送方式被淘汰,而在團山水廠"湖改江"中改、擴建單位費較高的輸送方式被淘汰,這表明所確定的輸送方式并不存在一致性偏向問題。
6.2.2單元素參數靈敏度分析結果(因篇幅所限,多元素參數分析及離散變化分析結果省略).
在保持原模型實例所求最優基仍為最優的條件下,各輸送管道及轉壓站輸送水量允許變化范圍如下:南湖北路DN1200管,三環路轉壓站,天泉路DN300管:0—+∞;南湖北路轉壓站,湖邊泵站,三環路DN400管,南湖南路DN800管,關山路轉壓站,關山路延長線DN1000管,蚌潮路DN300管,民院路DN400管,魯巷廣場DN800管分別為:0—1.3,0—1.3,0—1,0—1,0—6,0—1,0—2.5,0—1,0—2.5。
參考文獻
[1]IGNIZIO,J.P “Goal programming:A pool for multiobjective Analysis”,Journal of operational Research,Vol,29,Ⅱ,1978.
[2]J.P.Ignizio,閩仲求 《單目標和多目標系統線性規劃》上海:同濟大學出版杜,1986.
[3]韓旭昆《線性覿劃靈敏度分析》,系統工程,1992.(1).
[4]潭浩強,《C程序設計》,北京:清華大學出版社,1991.
作者簡介:
楊曉安(1968—),男,漢族,湖南人,工程師,碩士,研究方向為城市供水管網優化,武漢市自來水公司。
論文搜索
發表時間 至
月熱點論文
論文投稿
很多時候您的文章總是無緣變成鉛字。研究做到關鍵時,試驗有了起色時,是不是想和同行探討一下,工作中有了心得,您是不是很想與人分享,那么不要只是默默工作了,寫下來吧!投稿時,請以附件形式發至 paper@h2o-china.com ,請注明論文投稿。一旦采用,我們會為您增加100枚金幣。








