何義亮1，顧國維2
(1.上海交通大學環境科學與工程學院，上海200 240；2.同濟大學環境科學與工程學院，上海200092)

　　摘 要： 膜生物反應的實質是生物降解與膜分離相互影響、共同作用的過程。膜對活性污泥混合液的分離過程是由“兩次分離”實現的：一次分離是混合液在壓力作用下進行固液分離，二次分離是分離出來的液相透過沉積層到達膜表面，實現有機物大分子及膠體物質與水的分離。固液分離過程可用阻力模型來描述；而膜表面有機物大分子與水的分離可用凝膠極化模型描述。穩態時，固液分離的速率與有機物大分子和水分離的速率相等。
　　關鍵詞：膜生物反應器；兩次分離；數學模型
　　中圖分類號：X703.1
　　文獻標識碼：B
　　文章編號： 1000-4602(2001)02-0022-03

　　膜生物反應器是由超(微)濾膜組件和生物反應器構成的。傳統超(微)濾過程的進料一般為單相流體(即只有液相)，而膜生物反應器中超(微)濾分離的活性污泥混合液卻是固—液兩相流體，既包括活性污泥懸浮固體，也包括液體以及溶解在其中的有機物質，膜不但要截留大分子有機物，而且要分離固體顆粒。因此，固體顆粒在錯流中的遷移規律(包括固體顆粒在剪切流中的運動規律以及固體顆粒在膜面的沉積規律)就必然會對整個膜分離過程產生影響，對此過程進行分析并建立新的數學模型加以描述是十分有意義的。

　　1 固體顆粒在錯流過濾中的遷移規律

　　在錯流過濾中，固體顆粒的運動受沿膜面平行流動的剪切流和垂直于膜面的過濾滲透流的共同作用。滲透流趨向于將固體顆粒曳向膜面，而剪切流力圖保持顆粒懸浮，將其隨循環液帶出膜面。固體顆粒是沉積于膜面還是隨循環液流出，取決于剪切流和滲透流曳力的相互作用結果。
　　固體顆粒遷移運動趨于膜面的速率和流出膜組件的橫向遷移速率應該和顆粒直徑、流道幾何尺寸、剪切流速率和膜滲透過濾速率有關。
　　借用Alter和Belfort固體顆粒在錯流微濾過程中的遷移機理^［1］，對于達到穩定狀態時，即膜面的滲透過濾速率保持穩定時，顆粒遷移運動趨于膜面的速率為：

　　V_P=V_m［g(β)+R_ewh₂(β)］ (1)

　　式中　VP——顆粒遷移運動趨于膜面的速率
　　　　　Vm——膜滲透過濾速率
　　　　　Rew——滲透系數
　　　　　β——流道無量綱寬度
　　　　　g(β)、h2(β)——β的函數
　　顆粒橫向遷移速率為：

　　V_e=R_ep(d_p/2B)²u_mf(β ) (2)

　　式中　Ve ——顆粒橫向遷移速率
　　　　　um——流道剪切流速率
　　　　　dp——顆粒直徑
　　　　　B——流道寬度
　　　　　Rep——系數
　　　　　f(β)——β的函數
　　由式(1)、(2)可見，顆粒遷移運動趨于膜面的速率與膜滲透過濾速率成正比；顆粒橫向遷移 速率與流道剪切流速率成正比。

　　2 固體顆粒沉積阻力模型的建立

　　錯流過濾中，固體顆粒在過濾滲透流和剪切流的綜合作用下，有向膜面沉積的趨勢。隨著過濾的進行，會在膜面逐步形成沉積層。沉積層累積阻力Rd可由下式確定：

　　Rd=αd·Md (3)

　　式中　Rd ——固體顆料沉積層累積阻力
　　　　　αd——比阻
　　　　　Md——沉積負荷(單位膜面積的沉積量)
　　比阻αd可由Kozeny—Carman關系計算［2］：

　　αd＝180(1-ε)²/（d_s²ε³） ( 4)

　　式中　ε ——沉積層孔隙率
　　　　　ds——固體顆粒粒徑
　　由式(4)可見，沉積層愈密實，固體顆粒粒徑愈小，沉積層比阻愈大。
　　比阻受操作壓力P的影響，并有：
　　α_d＝αd₀·Pⁿ (5)

　　式中　αd0——系數
　　　　　n——壓縮系數
　　由超濾過程的阻力模型［3］得膜通量為：

　　J_v=P/μ(R_m+R_d)=P/μ·R _總 (6)

　　式中　Rm ——膜本身的阻力
　　　　　Rd——累積阻力
　　　　　R總——總阻力
　　　　　P——膜組件的操作壓力
　　　　　μ——動力粘滯系數
　　將式(3)、(5)代入式(6)中，有：

　　Jv=1/μ（P/（R_m+αd₀M _dP_n）） (7)

　　當操作壓力較大時，Rm＜αd0MdPn，膜通量可近等于：

　　Jv=1/μ（P^1-n/αd₀ M_d ） (8)

　　由于在操作壓力較大時已形成凝膠層，在此情況下，Jv已基本與P無關，亦即相當于n＝1，故式(7)可簡化為：

　　Jv=1/μ[P/（R_m+αd₀M_dP）] (9)

　　3 “兩次分離”模型的建立

　　在膜生物反應器中，膜分離不僅要實現活性污泥混合液的固液分離，而且還要實現大分子有 機物與水的分離。因此提出膜生物反應器的“兩次分離”觀點：
　　①膜對活性污泥混合液的分離過程是由兩次分離實現的，一次分離是混合液在壓力作用下進行固液分離，即混合液中的液相與活性污泥的固體顆粒分離，其相當于一個壓縮脫水過程，水中的溶解性有機物及部分膠體物質隨液相分離出來，而固體顆粒則在其遷移運動中逐步形成沉積層。二次分離是分離出來的液相透過沉積層到達膜表面，實現有機物大分子及膠體物質與水的分離。大分子有機物被截留在膜面形成濃差極化并逐步發展為凝膠層，水透過膜形成透過液。
　　②固液分離過程可用阻力模型來描述；而膜表面有機物大分子與水的分離可用凝膠極化模 型描述。
　　③穩態時，固液分離的速率與有機物大分子和水分離的速率相等。
　　上述假定用圖1表示。

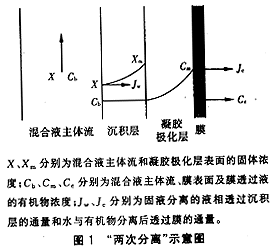
　　根據上述假定，固液分離過程可表述為：

　　J_w=1/μ[P/（R_m+αd₀M_dP）] (10)

　　要描述膜表面有機物大分子與水的分離，根據超濾分離的凝膠極化模型^［3］有：

　　Jc=kln（Cm-Ce）/（Cb-Ce） (11)

　　式中　k——物質遷移系數
　　令Jw=Jc，有：

　　1/μ[P/（R_m+αd₀M_dP ）]＝kln[（Cm-Ce）/（Cb-Ce）] (12)

　　引入膜對溶質的表觀分離率R=1-（Ce/Cb） ，代入式(12)并整理得：

　　Cm/Cb=R｛exp［（1/μ·k）( P/R_m+αd₀M_dP)］-1｝+1 (13)

　　若Ce足夠小，則有：

　　Cm=C_bexp［（1/μ·k）(P/（R_m+ αd₀M_dP)］ (14)

　　式(13)、(14)綜合地反映了膜生物反應器中，膜分離活性污泥混合液時固體顆粒的沉積和大分子有機物的濃差極化之間的相互作用，體現了操作條件(膜面流速u含在k中)與有機物濃度之間的相互關系，可以作為描述膜生物反應器“兩次分離”觀點的數學模型。
　　膜生物反應器“兩次分離”觀點的提出及其數學模型的建立，主要是依據理論分析，如何進一步驗證該觀點及其數學模型并使其具有可操作性，尚需在分子水平上對膜生物反應器的分離機理進行深入研究。

　　參考文獻：
　　［1］方為茂.十字流微濾過濾機理研究評述［J］.過濾與分離，1997，(3)：7-13 .
　　［2］張志誠. 超濾技術研究與應用［M］. 北京：海洋出版社，1993.
　　［3］葉凌碧.膜分離技術基礎［M］.北京：科學出版社，1989.

---

電 話：(021)64920310
收稿日期：2000-09-31