懸濁液透光脈動顆粒在線檢測技術及其應用(一)
于水利,李圭白,田永平
(哈爾濱工業大學市政與環境工程學院,黑龍江 哈爾濱150090)
摘 要:在國外現有研究的基礎上,從理論上推導出了懸濁液透光率脈動值的解析式。對該解析式的進一步研究表明,懸濁液透光率脈動值VR或R(R=VR/V)主要與懸濁顆粒大小有關,顆粒個數濃度N對VR或R的影響較小,懸濁顆粒凝聚時透光率脈動值總是增大的。給出了單一粒徑組成和具有一定粒徑分布的懸濁液,根據其透光率脈動值計算顆粒平均粒徑的解析式。
關鍵詞:懸濁液;透光脈動;懸濁顆粒;檢測;傳感器
中圖分類號:X832
文獻標識碼:A
文章編號:1009-2455(2001)01-0001-05
An On-Line Monitoring Technique for Transmitted Light Fluctuation
in High-Turbidity Water and Its Application
——A Theory of Monitoring for Transmitted Light Fluctuating Particles
YU Shui-li,LI Gui-bai,TIAN Yong-ping
(Sch.of Municipal & Environ. Engin.,Harbin Insistute of Technology,Harbin 150090,china)
Abstract:Based on the present research abroved, an analytical formula for transmitted light fluctuation (TLF) value of suspension liquid id deduced theoretical.Further research into this analytical formula shows that the TLF value of VR or R(R=VR/V) of suspension liquid is primarily related to the sizes of suspended particles while the concentration of the number of the particles has less influence on VR or R, and that TLF value always increases when suspended particles coagulate. An analytical formula is given to calcuate the average value of the size of the particles of a given suspension liquid having single particles size on the basis of its TLF value.
Key words:suspension liquid;transmitted light fluctuation;suspended particle;monitoring;transducer
前言
懸濁顆粒的檢測,目前國內外常用以光學檢測為基礎的各種光散射計數器,如:Coulter顆粒分析儀[1]及Hiac計數器[2]等。這些方法存在受光照射水樣體積小,檢測的只是單個粒子的行為,并需對檢測結果進行脈沖高度分析,不能實現在線連續檢測,
測定時需要對水樣進行稀釋,以避免顆粒的重疊,以及絮凝體在通過Coulter孔口或Hiac計數器的檢測區時被打碎,測定費時費力等問題。20世紀80年代后期,Gregory和Nelson[3]首次發現懸濁液透光率脈動值與懸濁顆粒粒徑有關,并就該相關關系進行解
析,從而為懸濁顆粒粒徑檢測傳感器研究開辟了新的途徑。
本文在國外透光脈動研究的基礎上,進一步對透光脈動理論進行探討,從理論上搞清了透光脈動值與懸濁顆粒的粒徑、分布及濃度的關系。
1 透光脈動懸濁顆粒檢測理論
1.1 懸濁液濁度
懸濁液濁度通常是通過測定其透光強度來確定的,因此其濁度大小取決于單位體積懸濁液內雜質顆粒數目及顆粒的光散射特性。對單一粒徑組成的懸濁液,假設單位體積懸濁液中有N個顆粒,顆粒的光散射截面為C;則當一束光通過長度為L的懸濁液的透過光強度I為:
I=IOexp(-NCL) (1)
式中IO為入射光強。式(1)即為Lambert-Beer定律。
濁度τu的定義為:
τu=NC (2)
由式(1)、式(2)得
τu=(1/L)ln(I0/I)
濁顆粒的光散射截面C,可用顆粒的幾何橫截面積表達,對于球形顆粒其表達式為:
C=Qπα2 (3)
式中:α-球形顆粒半徑;
Q-顆粒光散射系數(無量綱),其主要取決于光波長、顆粒大小及折光率。某些特殊情況下,Q可以簡單地計算出。
對有粒徑分布的懸濁顆粒,式(2)變為:
τu=∑NiCi
式中:Ni-i種顆粒的個數濃度;
Ci-i種顆粒的光散射截面。
1.2 懸濁液濁度變化理論
1.2.1 懸濁顆粒個數濃度的變化
連續式濁度計測量濁度時,即使同一個水樣其濁度測定值也隨機波動,原因是水樣的不斷更新,導致光路內顆粒個數濃度的隨機變化。
懸濁顆粒個數濃度N的這種隨機變化,主要是由兩方面的原因引起的,一是懸濁液中顆粒作布朗運動,使單位體積內顆粒數目產生隨機變化,并且該隨機過程可以用泊松分布描述。若單位體積內顆粒的平均個數為γ,則實際測量的顆粒數目為η的概率為:
p(n)=exp(-γ)·γn/n!
泊松分布的均值與方差相等,即懸濁顆粒數目的均值與方差均為γ,標準偏差為γ1/2,并且γ值較大時(γ>50),分布基本對稱并能以高斯分布估計。二是由于懸濁液中雜質顆粒濃度分布的不均勻性引起單位體積內顆粒數目的隨機變化,其隨機過程也可以用泊松分布描述。
對一定體積懸濁液中顆粒數目變化檢測的難易程度,在很大程度上取決于檢測樣品體積的大小,取樣體積越大,顆粒數目相對變化越小,越不易檢測;相反,取樣體積較小時,顆粒數目相對變化值較大,測定較容易。對一般的懸濁液,假定每單位體積內的顆粒數目N為108個/cm3,從一個混合良好的懸濁液中連續取1cm3的樣品,則由于樣品中的顆粒數目的變化遵循泊松分布,所以上述1cm3的連續樣品中,顆粒的平均數目為108個,標準偏差為104,樣品中含有的顆粒數在108±2×104之間的概率為95%。這個差異僅為平均值的0.02%,不易檢測到。然而,如果取很小的樣品體積,如0.1mm3,則樣品中顆粒數目的均值為104個,標準偏差為100,連續的樣品中的顆粒數目在均值上有±2%的差異,這就很容易檢測到。
1.2.2 懸濁液濁度的變化
懸濁液透光率的變化如圖1所示。一狹窄光束照射流動的懸濁液,透過光強由光電管接受并轉換成電壓信號。

由于光路中的顆粒使光產生散射(也可能是吸收),導致透光強度減弱。若光路長為L,光柱的有效面積為A,檢測水樣的體積為AL,則光路內顆粒的平均個數γ=NLA,則由式(1)得透光強度的表達式為:
I/I0=V/V0=exp(-γ·C/A) (4)
式中:I-平均透光強度;
IO-入射光強;
V/VO與I/IO相對應;
VO-相應于入射光強度的電壓;
V-相應于平均透光強度的電壓(直流)。
由于光路內的懸濁液不斷更新(流動的水樣),顆粒數目隨機變化(泊松分布),所以透光強度相應隨機脈動(參見圖1)。透光強度的這種變化可以用透光強度脈動值的均方根表示,相應的電壓脈動值的均方根為VR;其大小與光路內顆粒數目及其大小的隨機變化情況有關。
假設顆粒數目的隨機變化遵循油松分布[3],并且光柱內顆粒數目在均值上下一個標準偏差內波動。則通過計算光柱內顆粒數目的上限和下限值對應的平均電壓V,即可計算得到VR。計算時認為上限電壓與下限電壓之差是實際電壓變化的標準偏差的2倍,于是由式(4)得:
VR=VO[exp(-γC/A)](γ1/2C/A)
=V(γ1/2C/A) (5)
對于低濁懸濁液,V≈VO,則式(5)簡化為:
VR=VO(γ1/2C/A)
1.2.2.1 顆粒個數濃度對VR的影響
式(5)用顆粒個數濃度(N)表達為:
VR=VO[exp(-NCL)](NL/A)1/2·C (6)
對給定的裝置,L/A為常數,對顆粒個數濃度N很小的懸濁液,exp(-NCL)≈1,這時VR只與N1/2及顆粒大小(通過光散射截面C反映)有關,對固定大小的顆粒而言,VR隨顆粒的個數濃度的平方根成比例變化(圖2)。當N較大時,exp(NCL)開始對VR有影響。當指數部分減小的速度大于N1/2增加的速度時,VR達到最大值,對應的顆粒個數濃度Nmax=1/2CL這時V/VO=0.607。濃度繼續增大,VR開始減小。直流電壓V按指數規律隨N增大而減小(如圖2)。
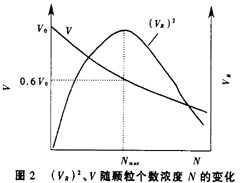
綜合式(4)和式(6)有
VR/V=(NL/A)1/2·C (7)
等式左邊是脈動電壓與平均電壓的比值,該比值隨顆粒個數濃度的平方根不確定地增加,其具體特性,很大程度上依賴于顆粒的特性(C值)。應用中將該比值用R表示,該比值不受取樣管管壁污染及電子元件漂移的影響,受影響的只是與平均透光強度對應的平均電壓V。
1.2.2.2 顆粒大小對VR的影響
為了討論顆粒大小對VR的影響,做如下假設:①懸濁顆粒體積濃度為SV;②懸濁顆粒為單一粒徑組成;③顆粒為球形,半徑α0則N=3SV/4πα3結合式(3)和式(7)有
![]()
式(8)中,設SV=10-3,A=3.42×10-2mm-2,L=1mm,光波長820nm,懸濁顆粒選聚苯乙稀,Q可根據mie理論計算,則按式(8)即可計算得到VR/V與顆粒粒徑的關系(圖3實線)。
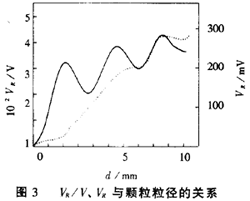
圖3中VR/V隨粒徑增大迅速增大,但出現一系列間隔規則的極大值和極小值,不過總的趨勢是VR/V隨粒徑增大而增大。
圖3中的虛線為VR的計算結果。這里
VR=VO[exp(-3QSVL/4α)]×(3πSVL/4A)1/2·a1/2·Q (9)
由圖3可見VR隨粒徑增大有規律地增大,曲線波動較小。這主要因為式(9)比式(8)附加了濁度及其隨顆粒大小變化一項。
對實際有一定粒徑分布的懸濁顆粒而言,式(7)變為:
R=VR/V=(L/A)1/2·(∑NiCi2)1/2 (10)
式中Ni是散射截面為Ci的顆粒個數濃度,求和是考慮了各種大小顆粒的綜合影響。
較小粒徑的顆粒,其散射截面較小,相應的NiCi2值也較小;而較大顆粒的光散射截面相對較大,即使其顆粒濃度較低,但也能得到較大的NiCi2值,對R值的貢獻相對要大些,所以,式(10)中R值的大小主要由顆粒的大小決定。在懸濁液中若有少量大顆粒雜質或懸濁顆粒產生絮凝時,由于大顆粒的存在或絮凝的形成會使R值顯著增大,因此,R值可作為反映懸濁顆粒混凝程度的指標。
當顆粒粒徑連續分布時,式(10)中的NiCi2項可用積分代替。假設不同粒徑顆粒數目的隨機變化是不相關的,并且都遵循泊松分布,則顆粒個數濃度脈動的總方差恰好就是每種粒徑顆粒單獨方差之和,于是對粒徑分布為f(a)的懸濁液,式(10)變為:
R=VR/V=(N·L/A)1/2π[∫0∞α4f(α)Q2(α)dα]1/2 (11)
式中N同前,Q(α)是半徑為α的顆粒的光散射系數。
1.2.2.3 顆粒凝聚或絮凝對VR的影響
懸濁液中顆粒產生凝聚或絮凝時,一方面,懸濁顆粒數目會減少;另一方面,其光散射截面增加。這兩種變化對VR和R有相反的影響,不過顆粒個數濃度的變化比聚集狀態的變化對VR和R的影響要小得多。
為了說明這一點,考慮兩個簡單的顆粒凝聚模式(如圖4所示)
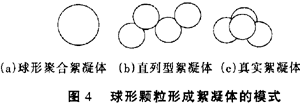
第一個模式,假設球形顆粒凝聚后形成更大的球形絮凝體[圖4(a)],光散射截面假設與顆粒的幾何截面積成比例,則
Cj=j2/3C1 (12)
式中:Cj—j重絮凝體的光散射截面;
C1—初始顆粒的光散射截面。
第二個模式,假設球形顆粒凝聚后形成直列形絮凝體[圖4(b)],則其總散射面積就是組成該絮凝體的那些初始顆粒各自散射截面積的總和
Cj=jC1(13)
不過,對許多情況,這些假設是不真實的,但它們可以作為極端情況,真實絮凝體的情況介于它們之間[圖4(c)]。
初始為單一粒徑組成的懸濁液在凝聚時可產生一系列粒徑的絮凝體,其分布情況取決于凝聚條件。為便于說明,假設絮凝體粒徑分布可用Smolu-chowski式表達,則在不同的無量綱時間t/tf(t為絮凝時間;tf為顆粒濃度減少到初始值的一半時的時間)值下可算得各種絮凝體濃度,將該計算值和式(12)或式(13)一起代入式(10)就可求出相應的R值。
未絮凝時,單一粒徑組成的顆粒,其R值可表達為
R未絮=(L/A)1/2·N01/2C1 (14)
對絮凝時有一定粒徑分布的絮凝體有
①顆粒形成球形絮凝體
R絮=R未絮{∑[(t/tf)j-1/(1+t/tf)j+1]·j4/3}1/2 (15)
②顆粒形成直列形絮凝體
R絮=R未絮{∑[(t/tf)j-1/(1+t/tf)j+1]·j4/3}1/2 (16)
用相似的方法可由式(4)推導出懸濁顆粒按上述兩種假設模型絮凝時,各自在絮凝前后濁度值變化情況的表達式。圖5為兩種假設模型各自的R絮/R未絮和τu絮/τu未絮隨絮凝進行其變化情況的計算結果。
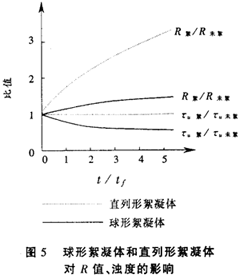
對形成直列形絮凝體的假設,凝聚發生后,濁度不變化,因為這時絮凝體散射的光與初始顆粒散射的光相同,但此時R值顯著增加;對球形聚合假設,當顆粒凝聚時,濁度明顯降低,而R值卻有相當比例的增大。
圖5中所示的兩種凝聚假設條件下的R值相對變化曲線是兩種極端的絮凝情況。實際中普遍存在是隨機形成的絮凝體,其R值變化曲線應介于這兩條曲線之間。由此可見,無論絮凝體的結構如何,當發生絮凝時人值總是增大的。
2 懸濁顆粒粒徑分析
式(4)兩邊取對數,并用N描述
ln(V0/V)=NLC (17)
由式(7)和式(17)消去顆粒的光散射截面C(顆粒的復雜函數),可求得懸濁顆粒個數濃度
![]()
若顆粒的體積濃度SV已知,則由式(18)可求出顆粒等體積球半徑α
![]()
式(19)只適用于單一粒徑組成的懸濁液。
對于具有一定粒徑分布的懸濁顆粒[其粒徑分布函數f(a)],結合式(3),式(17)可改寫為
![]()
由式(11)、式(20),即可得到具有一定粒徑分布的懸濁顆粒的個數濃度
![]()
同樣,若懸濁顆粒體積濃度為SV,則由式(21)可求出懸濁顆粒的平均體積粒徑α。
![]()
總之,對單一粒徑組成的懸濁液,顆粒個數濃度N可由懸濁液透光脈動檢測裝置方便地測出,而不需要知道顆粒的任何光學特性,尤其當顆粒體積濃度SV已知時,可定量計算出平均體積粒徑。對具有一定粒徑分布的懸濁顆粒,由該裝置也可以半定量地得到懸濁顆粒的個數濃度及其平均體積粒徑。
3 結論
透光脈動懸濁顆粒檢測技術與以往其它光學檢測法有本質的區別。透光脈動法重點考察的是懸濁液透光率的脈動值,并且該值通過光電轉換可以用輸出電壓的脈動值的均方根VR或R(R=VR/V)表示。懸濁液透光率脈動值VR或R(R=VR/V)主要與懸濁顆粒大小有關,顆粒個數濃度對VR或R的影響較小。對單一粒徑組成的懸濁液,由透光率脈動值可以定量地計算出顆粒的個數濃度和顆粒粒徑,而不需考慮顆粒的任何光學特性。對于具有一定粒徑分布的懸濁液,則必須考慮粒徑分布函數。對懸濁顆粒的各種凝聚模式的分析結果表明,懸濁顆粒凝聚(或絮凝)總是使透光脈動值增大。由于比值R不受取樣管管壁污染及電子元件漂移的影響,受影響的只是與平均透光強度對應的平均電壓V,所以實際應用中可將R值作為檢測指標。
參考文獻:
[1]Kayode T O,Gregory J A.New technipue for monitoring alum-sludge conditioning[J].Wat.Res.,1988.22(1):85~90.
[2]Bryant R L.On-line control of coagulant dosage using the streaming current detector[J].Industrial Water Engineenng,1983,20(5):16~36.
[3]Gregory J.Turbidity Flctuations in flowing suspenslons[J].Colloid Interface Sci.,1985,105(2):357-371.
作者簡介:
于水利(1962-),男,教授,博士生導師,哈工大市政工程系主任。1962年10月生,1983年畢業于哈爾濱建筑大學市政與環境工程學院,長期從事給水排水、環境工程的教學和科研工作。
Email:ysihgdd@china.com
收稿日期:2000-10-16
*霍英東教育基金會青年教師基金(編號:070),湖北省廢物地質處置與環境保護重地實驗室開放研究基金聯合資助。
論文搜索
月熱點論文
論文投稿
很多時候您的文章總是無緣變成鉛字。研究做到關鍵時,試驗有了起色時,是不是想和同行探討一下,工作中有了心得,您是不是很想與人分享,那么不要只是默默工作了,寫下來吧!投稿時,請以附件形式發至 paper@h2o-china.com ,請注明論文投稿。一旦采用,我們會為您增加100枚金幣。








