冷卻塔設計的計算機運算程序
胡連江1,孫慧2,蔡廣3
(1.天津石化設計院,天津 300271;2.上海深圳物業發展有限公司,上海 201108;3.西北建筑工程學院,陜西 西安 710061)
摘要:開發的冷卻塔計算機運算程序,可以把專業人員從繁瑣的人工計算中解脫出來,同時運算精度也得以大幅度提高,同時介紹了計算方法的選擇優化和程序編制以及變量確定的一些技巧。
關鍵詞:冷卻塔; 設計; 運算程序
中圖分類號:TU991.42
文獻標識碼:C
文章編號:1000-4602(2000)12-0039-04
水的循環使用是節約用水的重要途徑,冷卻塔又是水循環使用的關鍵設備,從某種意義上講,冷卻塔技術是循環水技術的核心。冷卻塔的設計計算一直是專業人員比較棘手的工作,這是因為繁雜的人工運算是很困難的,而采用簡化算法精度又不夠。因此,冷卻塔計算機運算
程序的開發成功,為新型冷卻塔的研制和開發提供了條件。
1 冷卻塔的設計計算
冷卻塔的設計計算主要包括熱力計算和空氣動力計算兩個方面,程序運算框圖見圖1。
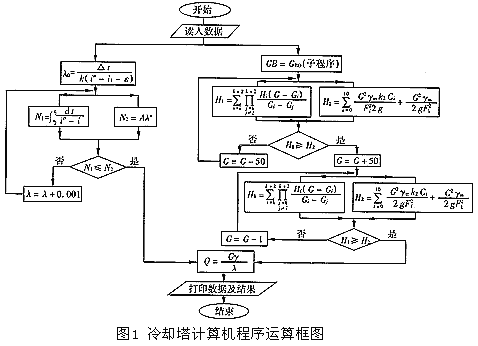
熱力計算目前廣泛采用的是麥克爾(Merkel)1925年提出的熱焓平衡及焓差方程,該方程從冷卻的角度描述了水傳熱和濕空氣吸熱過程的熱力特性,并由此演變出冷卻數N的方程[式(1)],它與J·李欽斯特(Lichtenstien)1943年從填料試驗中歸納出的填料散熱特性方程[式(2)]聯立求解,即可求得工作氣水比(見圖2)。
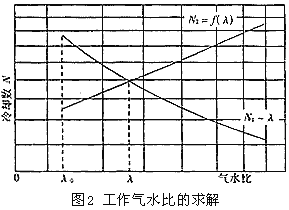
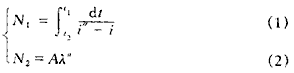
式中 N ——冷卻數
t1——進塔溫度
t2——出塔溫度
A——常數
λ——氣水比
i″——空氣飽和焓
i——空氣焓
n——常數
空氣動力學計算是通過對風機的特性方程[式(3)]和冷卻塔的阻力特性方程[式(4)]聯立求解,求得工作風量。風機的特性方程需由風機特性曲線擬合得來。
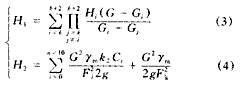
式中 H1 ——風機全壓
H2——冷卻塔阻力與全壓之和
γm——空氣的平均體積質量
k2——阻力系數
Ci——冷卻塔內各部位的阻力
Fi——冷卻塔內各部位的通風面積
Fk——風筒擴散筒上口的通風面積![]()
G——風量
2 計算方法的優化
2.1 冷卻數N
冷卻數N的表達式為積分式,對于積分的求解方法很多,其中經典的為辛普遜(Simpson)積分法。手算時一般采用簡化辛普遜法(辛氏三分之一法),此方法是以Δt/2為分割點,將曲線分成兩段,近似求解,但當Δt>15 ℃時計算誤差就會很大,簡化算法都難以滿足。為提高計算精度,在程序編制時應采用復化辛普遜法,數學原型為:![]() 。簡化辛普遜法只相當于復化辛普遜法m=1時的精度,當m=1000時,曲線將被分割為2000段,此時精度已達到千億分之一(辛普遜積分法的最大誤差值為(Δt/180n4|Δi|),計算機完成這些運算僅需3~4s,用這個結果去校驗手算值(上海科學技術出版社1981年的出版《冷卻塔》一書中的例題),均有3.9%~7.79%的誤差(見表1)。分析誤差產生的原因有三:一為公式因素,手算時n不可能取很大,一般取2,即簡化辛普遜法;二為取舍誤差;三為查表誤差。
。簡化辛普遜法只相當于復化辛普遜法m=1時的精度,當m=1000時,曲線將被分割為2000段,此時精度已達到千億分之一(辛普遜積分法的最大誤差值為(Δt/180n4|Δi|),計算機完成這些運算僅需3~4s,用這個結果去校驗手算值(上海科學技術出版社1981年的出版《冷卻塔》一書中的例題),均有3.9%~7.79%的誤差(見表1)。分析誤差產生的原因有三:一為公式因素,手算時n不可能取很大,一般取2,即簡化辛普遜法;二為取舍誤差;三為查表誤差。
數 氣水比λ 0.5 0.6 0.9 進塔溫度t1(℃) 40.24 40.24 40.24 出塔溫度t2(℃) 32 32 32 干球溫度θ(℃) 25.7 25.7 25.7 濕球溫度τ(℃) 22.8 22.8 22.8 大氣壓力(kPa) 99.658 99.658 99.658 結
果 手算冷卻數N 1.024 0.861 0.692 電算冷卻數N 0.95 0.807 0.666 差值(%) 7.79 6.69 3.9
2.2 風機特性方程
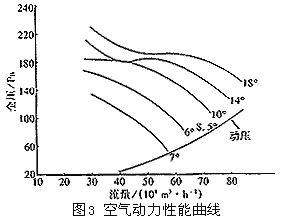
一般風機廠不提供風機特性方程,僅提供風機特性曲線,計算時需對風機特性曲線進行擬合。風機特性曲線擬合的方法很多,一般廣為采用的是二次拋物線法,其函數表達式為:H=ax2-bx-c(H為風機全壓,x為風量,a、b、c為常數),此方法直觀、簡便,在特定區間具有一定的精度,但缺點是局限性太大,因二次拋物線法函數的一階導數為H′=2ax-b,系單調函數,而風機特性曲線并非都具有一階導數單調性的特性,以4.7 m風機特性曲線為例(見圖3),當葉片角度≥14°時,曲線的一階導數不單調,曲線多次出現震蕩,特別是對風機原始參數分析結果表明,此種現象是經常的、大量的,因此用二次拋物線法描述風機特性是不理想的。
筆者在程序編制中采用了拉格朗日(Lagrange)一元三點插值法對風機特性曲線進行數值逼近,有效地避免了二次拋物線法的上述缺點,此法為分段二次拋物插值法,逼近效果優于經典拉格朗日插值法,且可避免經典拉格朗日插值法在高次插值時出現的龍格(Runge)現象。用風機廠提供的原始數據驗算此法,均方差為0.008%。其數學原型為:![]() 。
。
3 氣水比的計算
3.1 工作氣水比λ
工作氣水比λ系通過求解方程式(1)和(2)的聯立方程組求得工作氣水比。鑒于方程組為非線性方程組,直接求解很困難,程序運算一般采用試算法,先假定一個較小的氣水比λ0,代入式(1)求得N1值,代入式(2)求得另一個N2值。由圖2可見,當氣水比由小向大逼近時,聯立方程組有如下特性:在曲線的交點左側,N1>N2,隨著氣水比的增加,差值越來越小,直至N1=N2,即兩條曲線的交點就是聯立方程組的解,此時氣水比即工作氣水比。根據這一特性,循環終止條件可設置為N1≤N2,否則氣水比再加上一個微小值(步長),即λ=λ+Δ,重新代入式(1)、(2)計算,重新比較,直至求解。
3.2 初始氣水比λ0的確定
前述已知,氣水比是從一個較小的值向大值逐步逼近循環試算的,因此初始氣水比λ0就要足夠小,否則就有可能使方程越過兩條曲線的交點,致使聯立方程組無解,在程序運算過程中將形成死循環。然而從0開始又會增加很多無謂的運算,不必要。那么怎樣確定為最佳呢?分析出塔空氣焓的函數關系式:i2=i1+Δt/kλ,可知當λ變小時,i2就會增大,λ小到一定值時,i2將會增大到比進塔水溫t1所對應飽和空氣焓i″1還大,也就意味著此時空氣非但不能冷卻水,相反還要向水中散熱,這是與冷卻塔任務相反的工況,超出了冷卻塔焓差的定義域,也就是說i2大到極限趨近于i″1。因此可以假定i2=i″1-ε(ε為足夠小),此時的氣水比是趨近于最小極限的氣水比(具有實際意義值),即λ0=Δt/[k(i″1-i1-ε)。
4 風量的計算
4.1 工作風量的計算
冷卻塔風機工作風量的計算是計算風機在冷卻塔特定環境——特定的阻力、動壓、空氣密度及水量的條件下可提供的風量,同時確定工作風壓及此時的風機軸功率。風機工作風量是通過式(3)、(4)的聯立方程組求得。式(3)是風機全壓與風量的函數關系式,通過一元三點插值法對風機特性曲線擬合得來,對于該方程式直接求解目前還很困難,因此仍采用試算法。
鑒于從4.7 m到9.14 m風機的風量變化范圍較大(60×104~300×104m3/h),循環過程中較大的步長精度難以保證,小的步長對于大風機的風量計算來說,循環量又太大,因此宜將循環分成兩個階段,在第一階段采用大步長(Δ=50m3/h)以減少運算次數。假定風量由大向小逼近,聯立方程組在兩條曲線的交點右側應有H1<H2,隨著風量減少,差值越來越小,直至H1=H2,即兩條曲線的交點,也就是聯立方程組的解,此時的風量即工作風量。因此當H1≥H2時,兩條曲線已處于交點或越過交點,此時進入第二階段循環。為使程序循環進行下去,在第二階段循環的開始,應在第一階段循環的基礎上退回一步,即第一階段里每循環一步,風量將減去一個步長(Δ=50m3/h),完成第一階段的循環,此時的風量將作為第二階段循環的初始風量,但應先補回一個50m3/h,然后開始第二階段循環。第二階段采用小步長(Δ=1m3/h),這樣設置之后不僅提高了運算速度,而且計算精度也可控制在0.01%以下。
4.2 初始風量的設定
一元三點插值法對選取點的要求是必須在插值點所在的區間,即區間[最小插值點,最大插值點],否則函數會發生質的改變,也因此在確定初始風量時首先要滿足這個要求。由式(4)可知,塔內阻力與風量的平方成正比,程序可利用這一特性,先假定一個偏小的風量,代入式(4)后算出H(塔內的總阻力與動壓之和),持此值與風機全壓的最大插值點比較,若小于最大插值點,則風量加100m3/h,再代入式(4)循環試算,直至大于或等于風機全壓的最大插值點時,將此時的風量再減去100作為初始風量。
5 結語
冷卻塔計算程序的編制,使得繁鎖的冷卻塔計算變得輕而易舉,手算需要幾個工日的工作現在只需幾秒鐘,而且大大地提高了計算精度,這不僅為冷卻塔的計算提供了方便,也為新型冷卻塔的研制和開發奠定了基礎。幾年來,采用此程序對很多工程進行了計算,經測試表明,計算準確,結果可信。在此基礎上,并結合多年冷卻塔工程設計經驗,終于研制出“全流道流線型冷卻塔”(已獲得專利,專利號為:ZL 95 1 04965.8)。
參考文獻:
[1]李德興.冷卻塔[M].上海:上海科學技術出版社,1981.
[2]趙振國.冷卻塔[M].北京:水利電力出版社,1997.
[3]電子計算機算法手冊[M].上海:上海教育出版社,1982.
電話:(022)63804253
傳真:(022)25990266
E-mail:tpdinet@public.tpt.tj.cn
收稿日期:2000-06-08
論文搜索
月熱點論文
論文投稿
很多時候您的文章總是無緣變成鉛字。研究做到關鍵時,試驗有了起色時,是不是想和同行探討一下,工作中有了心得,您是不是很想與人分享,那么不要只是默默工作了,寫下來吧!投稿時,請以附件形式發至 paper@h2o-china.com ,請注明論文投稿。一旦采用,我們會為您增加100枚金幣。








