城市供水管網改擴建優化方法的研究
劉小靜 許仕榮 謝社平 何元春
(湖南大學土木工程學院水科學與工程系,長沙410082)
摘要 為克服一直以來城市供水管網系統改擴建優化工作的改造布局和離散管徑優化的兩大難題,本文采用模擬退火的玻爾茲曼機這一神經網絡技術進行求解,直接得到了市售管徑和優化的改造布局;整個系統采用系統工程的分解協調法來優化。
關鍵詞 供水管網 改擴建 優化方法
Abstract This paper adopts neural network technique of Simulated Annealing’s Boltzmann to solve the twain hang-ups in the rebuild and extend optimum work of city flow network since all along - the optimum of rebuild layout and scatter pipe-span. Then we can get the twain optimum results directly. Whole economy can be optimized by decomposing and corresponding divisor of systems engineering.
Key words flow network rebuild and extend optimum method
隨著我國給水事業的迅猛發展,各地市給水管網已具規模,但隨著人口增長和生活水平的提高,城市用水量急劇增長,管網系統滿足不了增長的用水量,在各方面存在一系列問題,從而適時、科學地對現有給水管網進行改擴建優化設計的研究,是城市供水行業亟待解決、有較高經濟效益和社會效益的課題。
供水管網系統改擴建優化設計問題,是在新建管網優化技術的基礎上更為復雜的含有混合整型離散變量的非線性規劃問題。以往的方法通常是在設計人員以經驗確定管線布局的條件下,采用連續變量的約束非線性優化方法求解該復雜的目標函數,再由連續最優解上下取整或通過目標函數轉換由連續變量優化方法求解。混合整型離散優化問題的特殊性使這種求解方法難以獲得原目標函數的最優解。
值得一提的是,改擴建又不同于新建,研究的不只限于新建管網的優化,其目標函數中也包含了舊有管段的因素,即有某些舊有管段的不合理存在,大大影響了整個管網的運行費用。從節能的角度,在擴建管段尋優的同時,要對不合理的舊管段進行改造,這勢必要增加基建投資(改造措施采用增敷平行管線的方法),那么其需要解決兩個問題:①在什么地方敷設新增管道;②增敷管線的經濟管徑怎么確定。這就存在一定的困難,主要表現在:①初始管網布局的確定比較困難;②人的經驗知識不易總結;③由于經驗知識的局限性,不易找出問題的最優方案。而擴建設計中新舊管道交錯,流量分配的作用非常復雜,用常規方法求解更是困難重重。從而如何對改造管道的布局尋優,如何在充分利用原有管道供水能力的情況下,對需改造、擴建的管網進行優化,比新建設計更為復雜,又是一道急需解決的難題。
給水管網是一個復雜系統,單憑市政工程的專業知識,不能圓滿地解決管網水力分析和設計運轉問題。在眾多的研究工作中已引入了其它學科的研究成果,如數學規劃、圖論、計算技術、最優控制、自動化、系統工程等,這樣可拓寬分析方法和研究范疇,發展新的理論和方法。
2.供水管網改擴建數學模型和計算方法
2.1 供水管網改擴建數學模型的建立
城市供水管網改擴建的優化設計問題,是在系統設計年限內最高日最高時用水量Qi( i=1,…,m )已知的情況下,確定新增(改造)管道的布局xij(i , j∈V)和參數Dij(i , j∈V),并確定各水源的供水量ui (i∈S),各節點的壓力Hi(i = 1,…,m)使得總的供水成本盡可能低。該優化設計問題的非線性規劃模型可歸納為:
min f ( H, D, x, u, Hp)
![]()
s.t. gi ( H, D, x, u, Hp) = 0 i = 1,…,m-1
![]()
![]()
Hi≥Himin i = 1,…,m
ui-uimin≥0 i∈S
uimax-ui≥0 i∈S
Dij∈W i , j∈V
HPij≥0 i , j∈V
![]()
式中:
D — 管徑(米)
l — 管線長度(米)
T ,T', T"— 管線、泵站、水廠的投資償還期(年)
P ,P',P"—管線、泵站、水廠的折舊與大修理費(%)
V—可布置改造和擴建管線位置的集合
a,b,α — 造價公式中的系數和指數, 隨管線材料和施工條件的不同而異
ri — i期供水能量變化系數,i = 1, 2, 3 分別表示供電高峰期、正常期和低峰期
Ei — 供電i期電價(元/kw.h)
Ti — 供電i期供水時間(h)
ui j ,ηi j — 分別為供電i期第j送水量(l/s)和泵站效率(%)
hi,j,k — 供電i期第j送水泵站至管網控制點管線上k管段的水頭損失(m)
ZC — 管網控制點要求的自由水壓值(m)
ZK — 凈水廠至管網控制點的某條線路的管段集
S — 所有泵站個數
E'—每千瓦容量加壓泵站造價(元/kw)
r'— 泵站機組儲備系數
η'— 泵站與輸電線效率(%)
mp — 泵站基建造價的經濟效應系數0<mp≤1
CK、CN — 分別為改建、擴建單位水量凈水廠(送水泵站)所需基建費用(元/ l/ s)
RK、RN—分別為改建和擴建凈水廠集
u0i— 第i凈水廠送水泵站原有最大供水量(l/s)
mr—凈水廠送水泵站基建經濟效應系數0<mr≤1
2.2 供水管網改擴建的計算方法
改擴建這個復雜的課題可用系統工程的大系統分解分層協調的方法分解成四個相關的子問題進行求解(其流程圖如圖1所示):
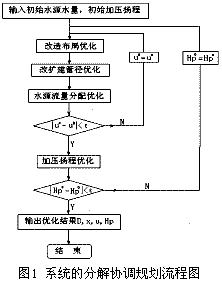
①在水源供水量和加壓揚程給定的情況下,對舊管網改造布局的優化子課題。它不同于新建模型優化的一點是,它的目標函數費用值不能計入整個系統的目標函數費用值中。
min f (H, D, x)
s.t. gi ( H, D, x) = 0 i = 1,…,m-1
Hi≥Himin i = 1,…,m
Dij∈ W i , j∈VV
Xij=0,1 i , j∈VVV
②若將u及Hp固定,節點數m不變,管徑數為需改造的管徑數及新建管徑數之和,此時舊管網改造布局的變量xij 已求得;則需改造和擴建管網的管徑優化子課題為:
min f ( H, D)
s.t. gi (H, D ) = 0 i = 1,…,m-1
Hi≥Himin i= 1,…,m
Dij∈ W i, j∈V
③設舊管網、需改造的管網及新建管網的集合為N;若將x,D及Hp固定,節點數m不變,管徑數為舊管徑數、需改造的管徑數及新建管徑數之和;則水源流量的優化子課題為:
min f (H, u )
s.t. gi ( H, u ) = 0 i= 1,…,m-1
Hi≥Himin i = 1,…,m
ui-uimin≥0 i∈S
uimax-ui≥0 i∈S
④若將x,D及u固定,節點數m不變,管徑數為舊管徑數、需改造的管徑數及新建管徑數之和n;則加壓揚程的優化子課題為:
min f ( H, Hp )
s.t. gi ( H, Hp ) = 0 i = 1,…,m-1
Hi≥Himin i = 1,…,m
HPij≥0 i , j∈V
3. 改擴建改造布局和管徑優化的模擬退火的玻爾茲曼機解法
3.1 模擬退火的玻爾茲曼機法簡介
從簡單的數學角度來求解改造布局和管徑優化的課題至今仍為管道技術的一大難關,而八十年代興起的人工神經網絡方法,在解決非線性優化問題上顯示的強大生命力,也給城市供水管網系統課題提供了新的啟示。
人工神經網絡是由大量簡單的神經元構成的并行分布處理系統。此問題實質上是在滿足一定約束的條件下,在并行分布處理網絡中搜尋最佳解的問題。對此,對Hopfield神經網絡賦予部分記憶矢量(部分約束)作為初值,網絡運行就達到某個局部最小點。該網絡中任何一對神經元之間的信息傳輸是雙向對稱的,它的基本工作原則是對網絡設置一個描述其狀態的能量函數E,該能量函數在系統狀態改變時總是減小,即dE≤0,系統必會到達一穩定點,其能量函數代表總花費。Boltzmann機神經網絡模型是在Hopfield網絡基礎之上引入隨機機制而形成的,具有較強的計算能力。與Hopfield網絡不同的是它具有學習能力,即其權值通過學習來調整,而不是預先設置,是一種約束滿足神經網絡模型。
模擬退火的Boltzmann機解法是在Boltzmann機中隨機地選擇一處理單元,通過系統狀態的改變,使系統的能量函數E朝其減小的方向遞減到一個穩定狀態,這個狀態往往是能量函數E的一個局部極小點,而達不到全局最優;再引入模擬退火算法,使整個系統產生振動,引導網絡達到其最佳平衡態,這就是搜索的最優解。
3.2 引用Boltzmann機進行改造布局和改擴建管徑優化的處理要點
①決策變量的轉換及神經元集合的構成
由于Boltzmann機的神經元狀態只能取0和1兩種狀態,需將獨立變量轉換成0-1變量。由于x本身就是0-1變量,無需轉換,只要將變量D轉換成0-1變量。對離散變量D,若它在集合W中可取的市售型號有M種,D的第ij維分量Dij用二進制字符串表示的最少符號個數m為2m≥M,Dij的取值與字符串S1"ΛS2"的取值一一對應。否則,若2m>M,字符串的取值多于Dij的取值,這時可以將多余的字符串的取值再對應于Dij的部分取值,使得每個字符串的取值對應的Dij的取值均是可行的。將D分量加上x分量構成神經元集合S。對于每一個Sij∈S,Sij∈{0,1},且S中的神經元元素的個數nl為 。
②能量函數
根據Boltzmann機的基本原理,改造布局或改擴建管徑優化的能量函數構造為。
式中:E—改造布局或改擴建管徑優化的能量函數
f1—改造布局或改擴建管徑優化的目標函數
A 一適當選取的正罰系數
③溫度T減小方式及計算過程的終止判據:在最優解的搜索過程中,溫度T由高溫逐漸降至低溫,其溫度T減小方式為T =λT,0 <λ< 1,根據經驗,筆者建議取λ= 0.8。當T → 0,即T<ε(ε是一小的正數)時,搜索最優解的過程結束,計算過程終止。
④狀態轉移的終止方式
在給定的溫度T,要進行多次搜索即狀態轉移,其狀態轉移方式為先以均勻分布在神經元集合中選擇一個單元,然后將其狀態作轉換,即若原來的取值為0,現在將其取為1,反之將其取為0。
⑤狀態轉移的終止判據
判斷狀態轉移是否結束可以有多種方法,如a) 檢驗目標函數值的均值是否穩定;b) 連續若干步目標函數值的變化均比較小;c)按一個固定的步數L進行狀態轉移等。這里選擇采用方法c)
3.3 Boltzmann機進行改造布局優化的電算方法
其方法是在優化結果中分析舊管網,如果計算管徑比實際管徑大,則考慮增敷一平行管線,即x的值取為1;否則,原有舊管徑處不變,即x的值取為0;并得到新的整體系統的總數(原有舊管徑、新建管徑和需改造管徑之和)。
值得注意的是,由該優化子課題得到的有用的結果只是需改造的舊管徑的地點,即改造布局優化,并不使用它求得的優化管徑。該優化子課題不參與總費用值的計算。其電算框圖如圖2所示。
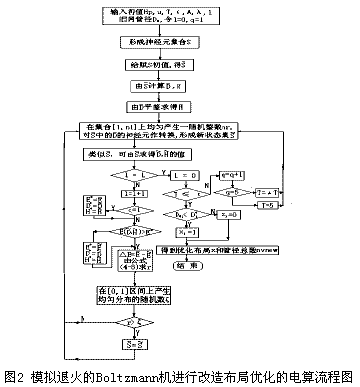
3.4 Boltzmann機進行改擴建管徑優化的電算方法
對于改擴建管徑的優化,其原理與改造布局優化一樣。它根據布局優化子程序輸入的管徑總數和改造布局,在原有舊管徑不變的情況下,求新建管徑和需改造管徑的優化結果。該子程序中,變量x為已知量,神經元集合S中只有神經元D。從而可得利用模擬退火的Boltzmann機進行改造布局優化的電算流程圖3。該算法計算獲得的并不一定是問題的全局最優解,但它是一個非常接近其全局最優解的局部最優解,其原因是:①由算法本身的特性決定的,該算法是以概率1保證其收斂到它的局部最優解,而不一定是全局最優解。②神經元的構造方法,包括編碼及精度,對算法的計算效果有一定的影響。
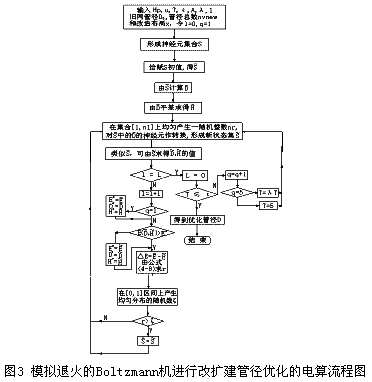
3.5 不同負載狀態下的布局和管徑的優化
在不同負載狀態下的布局和管徑的優化設計,采用模擬退火的Boltzmann機算法仍是易行的。當網內存在水塔水庫時,其運行上存在兩種狀態:①高峰用水期,水源和水塔水庫同時供水;②低谷用水期,單由水源供水并向水庫充水。此時,管線布局和管徑的計算要按高峰用水時和最大傳輸時的二種負載進行。所以,該優化設計計算子規劃目標函數為:
![]()
s.t. g/i ( H1, D, x , u1 ) = 0 i = 1,…,m-1
gi ( H, D, x , u ) = 0 i = 1,…,m-1
Hi≥Himin i = 1,…,m
Hi1≥Hi1min i = 1,…,m
Dij∈ W i , j∈VV
其中:H, Q ——最大轉輸時管網的節點壓力和節點流量
H1, Q1 ——高峰用水時管網的節點壓力和節點流量
Himin,Hi1min——分別表示最大轉輸時和高峰用水時管網各節點的最小允許壓力
g/, g — 分別表示最大轉輸時和高峰用水時管網的節點方程組
S — 最大轉輸時水源二級泵站個數
S1 —高峰用水時共同工作的二級泵站和水庫的個數
Cr,Cr1 — 分別包含能量變化系數v和 v1
v —— 年平均耗電能對最大轉輸時耗電能的比例
v1 — 年平均耗電能對高峰用水時耗電能的比例
關于它的算法,只需在前述算法中做一些改動:
①水源水量分配的初值為最大轉輸時u和高峰用水時u1兩項;
②在由D, u求H的同時,也由D , u1 求得H1;
③能量函數改為
![]()
這些改動表示D的變化必須兼顧二種負載狀態下動力費用的變化,通過能量函數的穩定可求得有效的結果。
4 改擴建水源水量和加壓泵站的優化方法
在改擴建管網設計中,因用水量增長必須增加水源的供水,由此產生了水廠供水的分配問題:①是否需要開辟新的水源;②如果需要新建水廠,新、舊水廠的供水量如何分配;③如果不需要新建水廠,在舊水廠之間如何分配這部分新增的水量。最優方案的選擇應使管網的常年動力費用(以發揮最大生產能力時的動力費用折算成年平均費用)和新建或擴建水廠所需的基建費用之總和為最小。
此外,由于給水面積擴大,用水需求加大,管線延長,管路的水頭損失將增加,為了保證邊緣地區的水壓,節約動力費用,管網內往往設置加壓泵站或水庫泵站。加壓泵站的優化設計就是研究如何選擇加壓泵站的個數、位置和加壓揚程使得管網的動力費用和新建加壓泵站的基建造價和為最小。
為解此兩大型優化方程組,考慮了幾個較為適用的主要優化算法:Mpop法解題的成功率很高,但尋找可行點的功能還不完善;Mulpen法有效性指標還不很令人滿意;GRG性能好,適應性強,解題成功率比較高,對于退化的全等式線性約束問題處理不好,但GRG法原理較復雜、算法龐大,對于大型優化問題有著較好的針對性。因而考慮用GRG算法來解決該數學模型是比較理想的。此兩個子課題的電算流程圖如圖4和圖5所示。
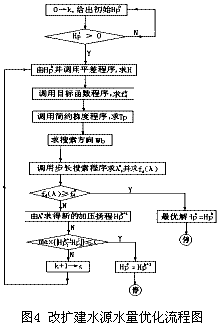
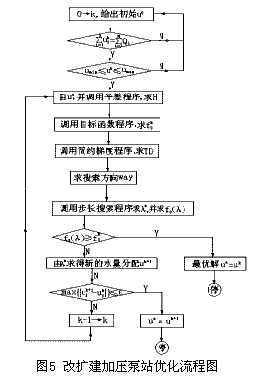
5. 工程應用與總結
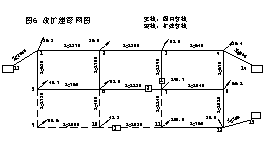
利用以上算法對長沙自來水公司的課題進行改擴建仿真計算;現以一簡例說明,如圖6所示。其計算過程列為表1。由計算結果可以看出,上述計算過程獲得了問題的全局最優解。對大規模的供水管網系統,該分層算法有顯著效果。
6. 參考文獻
[1] B.Coulbeck,Dynamic Simulation of Water Distribution Systems, Mathematics and Computers in simulation,1980,Vol.XXⅡ,222-230
[2] L.Gyergyek and S.Persen,Simulation and Optimal Control of Large Water Distribution Systems, Mathematics and Computers in simulation,1982,Vol.XXⅣ
[3] Neural Networks Based Decision Support in Presence of Uncertainties, Journal of water Resources Planning and Management,1999,No.5
[4] E.Aarts and J.Korst, Simulated Annealing and Boltzmann Machines,John Wiley & Sons,1989
[5] 全國供水管網論文集,1998
[6] 許仕榮,邱振華,給水管網的計算理論與電算應用,湖南大學出版社,1997
[7] 俞國平,給水管網擴建工程的最優化設計,同濟大學博士論文,1985
[8] 顏虎等,改造舊管網擴建方案可行性研究的方法,中國給水排水,1991
[9] G.V.雷克萊狄斯等,工程最優化—方法與應用,北京航空航天大學出版社,1990
[10] 陳立周等,工程離散變量優化設計法—原理與應用,機械工業出版社,1988
[11] 熊光楞,連續系統仿真與離散事件系統仿真,清華大學出版社,1987
[12] 仲偉俊,供水網絡系統改造的智能化計算機輔助設計,信息與控制,1995,6
[13] 李衛華,人工智能程序設計,科學出版社,1989
[14] 胡守仁,神經網絡導論,國防科技大學出版社,1993
[15 胡守仁,神經網絡實現技術,國防科技大學出版社,1993
[16] 胡守仁,神經網絡應用技術,國防科技大學出版社,1993
[17] 陳偉民,人工智能技術及應用,同濟大學出版社,1998
[18] 萬百五等,大工業過程計算機在線穩態優化控制,科學出版社,1998
作者簡介:
劉小靜(1975- ),女,湖南人,
電話:(0731)8828281
通訊地址:湖南大學研究生樓501室 410082>
注:該課題為長沙市自來水公司公關項目。
論文搜索
月熱點論文
論文投稿
很多時候您的文章總是無緣變成鉛字。研究做到關鍵時,試驗有了起色時,是不是想和同行探討一下,工作中有了心得,您是不是很想與人分享,那么不要只是默默工作了,寫下來吧!投稿時,請以附件形式發至 paper@h2o-china.com ,請注明論文投稿。一旦采用,我們會為您增加100枚金幣。








