城市給水管網優化設計方法與發展
信昆侖 劉遂慶
(同濟大學環境科學與工程學院)
摘要 本文簡要介紹了給水管網工程領域研究者所使用的傳統優化設計方法和最新發展,并對各種方法進行了簡單的比較,同時概要介紹了管網可靠度問題在模型中的實現。
關鍵詞 給水管網 優化設計 線性規劃 非線性規劃 可靠度
1 概述
自本世紀60年代提出給水管網設計優化計算方法以來,研究者在這一領域已經取得了長足的進展,提出和發展了基于最優化理論和管網水力特性的各種設計理論和方法。
最早給水管網設計模型是基于樹狀管網提出的(例如,kormeli et al(1968),schaake and lai (1969)),這些模型可以尋求全局最優解,然而由于其僅僅適用樹狀管網,因而對于在實際城市給水管網的設計者來說并無太大的價值。
2 線性規劃法
Alperovits and Shamir 于1977年提出所謂線性規劃梯度法,并給出了其在復雜管網系統以及多水力工況下的應用,也為以后研究者指出了一條逐步迭代逼近尋優的設計思路,奠定了兩階段法的基礎。以管網中無其他組件且是單一工況這一最簡單的情況為例:
對于已知的管網分布,預分配管網各管段的流量,對于管網中的各條管段,分別使其有連續幾段標準管徑的管段組成,各段長度記為Li,j (連接i ,j 節點管段中第m檔管徑的管段長度) ,構造以下經過簡化后的目標函數
![]()
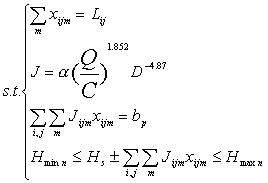 (1)
(1)
說明: Jijm:組成管段Li,j 的第m檔管段的水力坡度:
bp: 對于環路為0,對于已知端點水頭的路徑為兩端點的水頭差值
Hmaxn,Hminn分別是n節點所允許的最大最小水頭值
用經典的線性規劃方法容易求出該L.P.問題的最優解,至此完成兩階段法的第一階段。
第二階段是:計算目標值關于流量分配的梯度向量:
![]() (2)
(2)
構造第二階段目標函數
![]() (3)
(3)
該步驟中β的尋找是通過試算實現,即給定初始β值作為相對于最大梯度向量分量的Q值的增量并依次按Gp的比例計算對應Qp的增量,通過試算確定滿足該目標函數的β值,從而獲得該種管徑組合下的最優流量分配,重新回到第一階段,重新計算該流量分配下的管徑組合方案,如此往復直至目標值不再減少為止。
此后,Quindry 等(1981)提出與之相似的算法,不同的是其在第二階段通過調整節點水頭而不是流量分布逼近最優解。Okitsugu Fujiwara 和Do Ba Khang 于1990年提出綜合兩者交替固定流量分配和節點水頭逼近最優解,這些方法都是基于Xi,j為決策變量的線性規劃問題,并都對多工況,有泵站,水池及閥門的復雜管網系統進行了討論。
線性規劃方法是對于可行域內最優解的線性逼近,由于管網系統的優化結果傾向于管網樹狀化,加入最小管徑約束只能保證管網的環狀,并不能實現真正意義上的管網可靠性問題,因而如何在線性模型中實現可靠度的思想日益為研究者所關注。但是,由于可靠性的度量到目前為止還沒有公認的定義,因而所有關于可靠度的線性規劃模型問題并不具備統一的形式,也沒有廣泛的適用性,近幾年各國學者分別提出各自關于可靠度的模型,例如, Ian C.Goulter and Francois Bouchart 于1989 年提出的以下模型:
以rij表示單位長度的第i管段第j檔管徑的管段每年平均的破壞次數,加入以下約束:
![]() (4)
(4)
其中
![]() (5)
(5)
RHSi表示rij服從一定概率分布前提下給定時間內i 管段所允許的故障次數。
Kofiawumah,Ian Goulter 等于1991年提出以熵作為管網可靠度的代用度量:
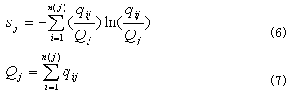
其中qij表示由第i點流入第j點的流量。
此外,Okitsugu Fujiwara等以事故時流量虧值與總需水量的比值、Heekyung Park(1993)以冗余度(redundancy)作為可靠度的度量等等不一而足。總之,可靠度由于其復雜的概念內涵(與管徑,管材,閥門的多少,管網的構成,故障的隔離與修復時間有關),因而現有的各種度量方式都不能涵蓋所有方面,考慮的越全面,受計算時間及計算速度的影響隨管網規模的遞增就越明顯。
3 非線性規劃方法
由于管網優化設計計算問題本身具有的非線性性質,因而也可直接采用非線性規劃法解決,對于有泵站情況,經簡化后的數學模型可寫為:
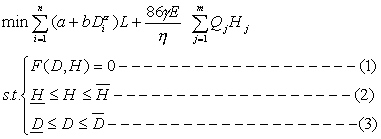 (8)
(8)
n-管段數;m-水源泵站數;a,b,α-管段造價公式系數;E-電費換算系數;γ-能量不均勻系數;η-泵站總效率;Li-管段長度;Qi-節點流量;Hi-節點水頭 H,D-節點水頭,管徑上限;F(D,H)=0-節點連續性方程。
由hazon-willianm公式![]() ,Hi可以表示為Di的非線性函數。于是上述問題轉化為以D為決策變量的非線性規劃問題,然而對于復雜系統F(D,H)=0將分解為相當龐大的約束集合,增加了用非線性規劃法求解的難度。目前,大多數學者傾向于采用獨立的水力計算程序求解該約束,這樣會大大削減主干問題的約束個數,利于非線性規劃方法的求解。具體到非線性規劃算法,應用最廣泛的是廣義簡約梯度法(General Reduced Gradient),其中以Lasdon和Waren于1983年開發的GRG2程序最為常用。水力計算程序使用最多的是Wood于1980年開發的KYPIPE(University of Kentucky Model)。
,Hi可以表示為Di的非線性函數。于是上述問題轉化為以D為決策變量的非線性規劃問題,然而對于復雜系統F(D,H)=0將分解為相當龐大的約束集合,增加了用非線性規劃法求解的難度。目前,大多數學者傾向于采用獨立的水力計算程序求解該約束,這樣會大大削減主干問題的約束個數,利于非線性規劃方法的求解。具體到非線性規劃算法,應用最廣泛的是廣義簡約梯度法(General Reduced Gradient),其中以Lasdon和Waren于1983年開發的GRG2程序最為常用。水力計算程序使用最多的是Wood于1980年開發的KYPIPE(University of Kentucky Model)。
對于模型中的約束(2),Lansey和Mays(1989,1992)、Ning Duan(1990)等采用了增廣拉格朗日乘子的處理方法。
設:![]() (9)
(9)
目標函數改寫為:
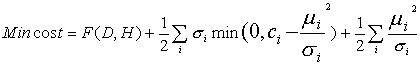 (10)
(10)
其中:ci=min(ci-ci),ci=Hi-Hi,Ci=Hi-Hi
μi—懲罰因子,σi —拉格朗日乘子。
此時該目標函數所對應的約束只有(3),大大減少了問題的規模.同樣,如果將管網可靠度看作H,D的函數,模型中可加入以下可靠度約束:
R(H,D)≤R(H,D)≤R(H,D) (11)
該約束的求解也多采用獨立子程序計算并以拉格朗日乘子的形式加入目標函數中以降低非線性規劃問題的復雜程度,三者的關系可以下圖表示:
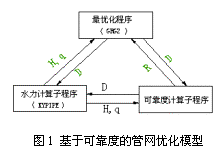
大量的研究者采用了GRG2、KYPIPE兩個子程序分別處理最優化部分和水力計算部分,因此各種非線性算法的主要分歧仍然落在可靠度計算子程序上.不同研究者分別采用了不同的度量方式 (最小切割集法,Su Yuchun,1988;RAPS程序,Ning Duan,Lansey,Mays,1990;時間比例法,Cullinane,Lansey,Mays,1992),類似于線性規劃方法,不同算法在或是計算時間或是概念涵蓋方面都有各自的缺點或長處而分別適用于解決某一特定類型的問題。
4 生物進化規劃及遺傳算法
近年來,隨著生物工程的蓬勃發展,隨之而起的遺傳學算法開始介入各個工程領域,該算法在有泵管網,管網擴建與改建等課題中也開始有應用(David.E.Goldberg,1987;Simpson 等,1995)。遺傳算法(Genetic Algorithm)應用于給水管網優化設計課題中,實質上是一種策略枚舉法,以單工況,單水源的簡單情況為例:
首先對工程實際所限定的各檔標準管徑進行編碼,于是管網不同的管徑組合方案可以形成不同的代碼串,經過對每一代碼串的解碼,由水力計算子程序可以求出該方案下管網的水力特性如H,Q等,進而可以求算用于評價方案優劣程度的目標函數值。然后遺傳算法根據生物遺傳進化的原理,對產生的初始方案進行選擇、重組、變異, 產生新一代個體,仿照生物進化過程代代進化下去,最終可以得到滿足要求的最優個體,解碼后即為該課題的最優方案。
相對于傳統的線性,非線性規劃算法,遺傳算法的優勢在于:(1)算法思路簡單,不受規劃問題要求的可微、可導、連續等限制,不但可以避免線性規劃解的”瓶頸”問題,也避免了非線性規劃最后對連續管徑進行”圓整”帶來的麻煩與偏差(2)由于遺傳算法從一組方案出發,擴大了搜索尋優的范圍,減少了傳統規劃方法線式尋優(如按梯度搜索)產生局部最優解與全局最優解差距較大的風險。遺傳算法的不足之處在于耗機時太多,對大型復雜管網更是如此.這主要由于其中的選擇,交換,變異等過程還沒有一個適合管網優化問題的完善算法,同時也是因為該算法貫串了幾率的思想而不似傳統方法具有確定性。
5.結語
隨著研究者在這一領域的不懈努力,給水管網優化設計計算的方法日趨豐富,涉及的問題的深度與廣度也日趨加強,具體地說,如何對復雜管網在多種工況時,考慮管網的可靠性情況下,利用原有的線性的或者非線性的方法,或者采用遺傳算法之類的新方法進行優化設計,使之更接近城市供水管網的工程實際,并進一步開發相應的軟件,是研究者所關注的課題。
參考文獻:
[1].I.C.Goulter(1990),”Systems Analysis in Water-distribution network design:From Theory to Practice”,J. Water.Res.Plan.Magmt,vol.118(3),238-248
[2].Alperovits E.,Shamir U.(1977)”Design of optimal water distribution systems”,Water.Resoures.Research, vol.13(6),885-900
[3].Okitsugu Fujiwara,Do Ba Khang(1990),”a two phase decomposition method for optimal design of looped water distribution networks”,Water Resources.Research,vol.26(4),539-549
[4].Ian C. Goulter,Francois Bouchart(1990),”reliability-constrained pipe network model”,J.Hyr.Eng.ASCE, vol. 116(2),211-229
[5]Kofi Awumah,Ian Goulter ,Suresh K Bhah(1991),”entrophy-based redundancy measures in water-distri- bution networks”, J.Hyr.Eng. ASCE,vol..117(5),595-613
[6]Okitsugu Fujiwara,Amal U. Silva(1990),”algorithm for reliability-based optimal design of water networks”, J.Env.Eng.ASCE.,vol .116(3),575-587
[7]Heekyung Part,Jon C. Liebman(1993),”redundancy-constrained minimum-cost design of water-distribution nets”,J.Water.Res.Plan.Magmt.ASCE,vol.119(1),83-99
[8].Kevin E.Laney,Larry W.Mays(1989),”optimization model for water distribution system design”, J.Hyr.Eng., vol.115(10),1401-1419
[9]Yuchun Su,Larry W. Mays,Ning Duan,Kevin E. Lansey(1988),”reliability-based optimization model for water-distribution systems”,J.Hyr.Eng.,vol.114(2),1539-1555
[10].Ning Duan,Larry W. Mays,Kevin E. Lansey(1990), “optimal reliability-based design of pumping and distribution systems”,J.Hyr.Eng.,vol.116(2),249-268
[11].Simpson,Dandy,Murphy(1995),”Genetic Algorithms Compared To other techniques for pipe optimization”, J.Water.Res.Plan.Magmt., vol.120(4),423-441
[12].David E. Goldberg ,Chie Hsiung Kuo,(1987),”Genetic algorithms in pipe optimization”,J.Comp.Civ . Eng.,vol.1(2),120-141
論文搜索
發表時間 至
月熱點論文
論文投稿
很多時候您的文章總是無緣變成鉛字。研究做到關鍵時,試驗有了起色時,是不是想和同行探討一下,工作中有了心得,您是不是很想與人分享,那么不要只是默默工作了,寫下來吧!投稿時,請以附件形式發至 paper@h2o-china.com ,請注明論文投稿。一旦采用,我們會為您增加100枚金幣。








