呂謀¹，張土喬¹，趙洪賓²

（1.浙江大學 市政工程研究所 2.哈爾濱工業大學 市政環境工程學院）

　　摘要：根據給水系統的網絡特性，并結合我國實際情況，對優化調度控制方法進行了系統的分析，進而提出了大規模混合實用優化調度模型及算法，并在城市供水系統中進行了實際應用，證明了其實用性。
　　關鍵詞：給水系統；混合優化；實用調度
　　中圖分類號：TU991
　　文獻標識碼：A
　　文章編號：1000-4602(2000)11-0010-05

Multi-Purposes Mixed Optimal Operation Schedule for Water Supply System
LU Mou¹,ZHANG Tu?qiao1,ZHAO Hong?bin²
(1.Institute of Munic.Eng.,Zhejiang Univ.,Hangzhou 310029,China;2.School of Muni
c.and Environ.Eng.,Harbin Institute of Tech.,Harbin 150090,China)

　　Abstract： According to the network characteristics of water supply system and the practical situation in China,an optimal operation schedule in water distribution networkwas analyzed,and then a practical mixed d- ispatch model and algorithm on large scale water supply system were put forward.The model was applied to urban water supply system and verified its practicability.
　　Keywords: water supply system;mixed?optimization;operation schedule

　　1 模型分析

　　優化運行控制問題就是為已定的配水系統提供科學合理的優化運行策略。根據所選決策變量的不同,可以建立供水系統決策的隱式模型和顯式模型^［1］。顯式模型中直接以實際水泵的運行作為決策變量；而隱式模型則是首先采用中間變量，如泵站、出口流速、水池變化軌跡等，并依此進行目標函數的尋優。隱式模型的求解精度較高，優化效果好，但計算耗時很長，對于泵站內水泵組合數較少，缺少調速泵，即泵站內可調余地較小的系統，有時得不到優化解。因為當一級尋優得到最優的流量分配后，泵站內有限的水泵組合種類不能滿足所需要的供水流量，就可能使泵站組合種類的可行域與最優流量可行域的交集出現空集，即出現無解的情況。顯式模型由于將整個系統統一考慮，一次求解，計算效率較高，但一次建模中考慮的變量及約束條件多，建模及運行復雜，當供水系統中的泵站可調余地小，尋優困難時，可考慮放松系統約束條件，以滿意解為追求目標，建立顯式優化決策模型，以保證優化調度的可行性。

　　2 定速泵站優化調度模型的建立

　　給水系統優化調度的目的，就是通過調整運行方案，在滿足水量、水壓要求的前提下，盡量使系統總運行費用達到最低^［2］。那么隨調度方案的不同而發生變化的這部分運行費用主要包括∶(1)制水成本 (2)泵站電耗。優化調度建模一般需要構造目標函數和約束函數，目標函數是指系統運行需達到指標的數學描述，即數學表達式；約束函數是指制約或控制系統運行的數學表達式，即優化運行必需滿足的前提和基礎。通常，供水系統優化調度模型是以運行費用為目標函數，以滿足管網水力特性方程及其他技術條件為約束進行系統整體優化的，因此目標函數應包括：
　　① 制水成本
　　由水廠藥劑費用及取水和凈水過程耗用的電費。數學描述為：

　　

　　式中　F₁——制水成本
　　　　　S_i,j——第i泵站第j時段單位制水費用(元/m³)　
　　　　　Q_i,j——第i泵站第j時段的出水量
　　　　　I——水源泵站數
　　　　　J——劃分的周期內時段數
　　② 泵站電耗
　　在計費計算中，一般只計直接費用，不計間接費用。可描述為：

　　

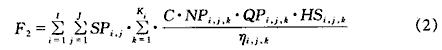
　　式中　SP_i,j——第i泵站第j時段的電度電費
　　　　　C ——換算系數
　　　　　NP_i,j,k——第i泵站第j時段第k種水泵開機臺數
　　　　　QP_i,j,k——第k種泵出水流量
　　　　　HS_i,j,k——第k種水泵出水揚程，可由Q～H特性曲線擬合其關系式
　　　　　η_i,j,k——第i泵站第j時段第k種水泵的計算效率，可由水泵效率曲線擬合其關系式
　　　　　K_i——i泵站水泵型號種類數
　　考慮供水系統運行的技術要求及為了更好地與實際系統相吻合，可考慮建立多目標優化調度模型，則技術目標包括：
　　① 供需水量差F₃最小

　　

　　式中　QF_j——j時段系統的總需水量(由用水量預測模型計算求得)
　　實際供水系統中，供需水量是平衡的，即：，也就是說，這應是優化模型中的一個硬約束條件。但為保證優化計算的可行性，可以將其軟化，放松約束限制，以擴大可行域，因此本文將，也作為優化追求的目標，在優化過程中逐步使_,逼近QF_j，最終得到優化目標的可行滿意解。實際應用發現，這種處理使優化程序的通用性及可靠性大大提高，是一種有效的實用方法。
　　② 泵站供需壓差F4最小

　　

　　H_i,j為第i泵站第j時段滿足配水管網用水量所需要的泵站出口壓力，其計算值可通過對供水網絡的運行分析，建立管網工況動態非線性模型得到，
　　即：H_i,j=F(Q_j,H_P,j)　　　　　　　　　　　(5)
　　式中　　Q_j——j時段各出水泵站的出水流量所組成的向量
　　　　　　H_P,j——各測壓點按時間序列分析所得到的壓力預報值向量
　　HP_i,j為第i水泵站第j時段能提供的出水水頭，其計算式由泵站內各水泵聯合工作的Q～H特性曲線擬合得到。實際運行的供水系統，應滿足供需水壓相等，即：H_i,j=HP_i,j，是優化模型中的硬約束條件，但由于與F₃相似的原因，這里也將其軟化，以作為優化追求目標，在優化過程中逐步使H_i,j逼近HP_i,j，最終得到優化目標的可行滿意解。
　　根據給水系統的特性，優化調度模型時還需要考慮約束條件，對于上述多目標決策問題，可采用多種優化方式，這里提出化多為一的乘除法，將多目標轉化為單目標問題求解。則建立城市供水系統的顯式優化調度模型如下：

　　

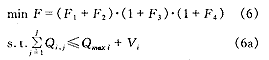
　　H_mini,j≤H_i,j≤H_maxi,j 　　　　　　(6b)
　　HS_mini,k≤HS_i,j,k≤HS_maxi,k 　　　 (6c)
　　QS_minj,i≤Q_i,j≤QS_maxj,i 　　　　　(6d)
　　NP_mini,k≤NP_i,j,k≤NP_maxi,k 　　　 (6e)

　　式中　N——測壓點數
　　　　　V_i——第i泵站調度日開始時段的儲水池有效儲量
　　　　　Q_maxi——一日內最大出水量
　　　　　H_mini,j——第i測壓點j時段最低運行服務水頭
　　　　　HS_mini,k——第k種水泵最低供水揚程
　　　　　HS_maxi,k——第k種水泵最高供水揚程，它們是由水泵特性曲線的高效區決定的
　　　　　QS_minj,i——i泵站j時段最低允許供水量
　　　　　QS_maxj,i——i泵站j時段最高允許供水量
　　　　　NP_mini,k——第i泵站第k種水泵最少開機臺數
　　　　　NP_maxi,k——第i泵站第k種水泵最多可運行數量。
　　所謂顯式調度模型是將整個給水系統結合在一起建模，經一次尋優直接得到最優的水泵運行決策方案。模型（6）中的目標函數中含有多個連續變量及離散變量，實際計算時，這里僅取HP_i,j及NP_i,j,k作為尋優決策變量，其他連續變量可以由它們解出。
　　Q_i,j求得后，利用式(5)可確定H_i,j。由此可見，當HP_i,j及NP_i,j,k確定后，其他變量便可唯一求得，因此式(6)可概括成：
　　min　F(NP_i,j,k，HP_i,j) 　　　　(7)
　　s.t. g(NP_i,j,k，HP_i,j)≤0
　　對于這種含有連續變量又含有離散變量的優化問題，我們在以離散搜索法為理論依據的MDOD方法^［3］的基礎上，經改進開發了求解混合離散變量的供水系統直接優化調度軟件（用C++計算機語言），程序計算框圖(見圖1)。

　　3 多水源含調速泵的優化調度

　　變速調節雖然是較為理想的調度形式，但相對于水泵價格而言，調速裝置的價格是昂貴的。因此，為了節省一次投資，經常采用恒速泵與調速泵并聯的方式，尤其是針對目前的國情，很多城市的二級泵站還沒有裝配調速裝置，因此混合泵站的優化調度具有很現實的意義。
　　由于與定速泵站相比，混合、變速泵站的可調余地大，應該對定速泵站和混合、變速泵站采取不同的處理方法，這里提出將隱式模型與顯示模型相結合，建立混合實用優化調度模型。為研究方便，設系統中含有定速泵站和混合泵站兩種類型(含有變速泵站的情況可參照混合泵站的情況解決)。即編號1，2，…，X為定速泵站，X+1，…，I為混合泵站，參照式(7)仍可建立混合供水系統調度運行的直接優化模型。其優化追求的目標仍然由F₁、F₂、F₃、F₄組成，設：[NP_1,j,k,NP_2,j,k,…，NP_X,j,k］^T=NPF,［QP_1,j,k,QP_2,j,k,…,QP_X,j,k］^T=QPF,［Q_X,j,Q_X+1,j,…，Q_I,j ^T=QV(j=1,2,…，J；k=1,2,…，K_i)
　　則：F₁=∑Xi=1∑Jj=1S_i,jQ_i,j+∑Ii=X+1∑Jj=1S_i,jQ_i,j　　　(8)
　　由于Q_i,j＝∑Kik=1NP_i,j,k·QP_i,j,k 　　　　　　　　　　　 (9)
　　式(8)等號右邊第一項由式(9)代入，第二項保持不變，即：
　　F₁=FF₁(NPF,QPF)+FV₁(QV)　　　　　　　　　　　　　　　　　(10)
　　F₂式也可分成兩部分
　　

　　式中　H_i,j——第i混合泵站第j時段泵站出口壓力
　　由式（5）可表達成各泵站出水流量的函數，則上式可表達成：
　　F₂=FF₂(NPF,QPF)+FV₂(QV,NPF,QPF)　　　　　　　　　　　　 (12)
　　結合式(9)，混合系統的技術性指標F₃可表示成：

　　

　　對于調速或混合泵站，在調節范圍內，對應于每一個配水管網所要求的泵站出口壓力，總可以通過調整調速泵的轉速使泵站供水揚程滿足管網需要，也就是說在滿足供水量的前提下，保證供需水壓平衡。在直接優化調度模型中，只把混合泵站的出口壓力及出水量作為決策變量來考慮，也就是說，尋優結果只是得到混合泵站的最優出水量及最優出水壓力，并沒有實際泵站內的實際運行策略，因此不存在供需水壓差最小這個指標。則F4可表達成：

　　

　　則混合供水系統的直接優化調度模型可表達成：
　　min F=(F₁+F₂)·(1+F₃)·(1+F₄) 　　　　(15)

　　
　　H_mini,j≤H_i,j≤H_maxi,j(i=1,2,…，N；j=1,2,…，J)
　　HS_mink≤HS_i,j,k≤HS_maxk(i=1,2,…，X；j=1,2,…，J；k=1,2,…,K_i)
　　QS_minj,i≤Q_i,j≤QS_maxj,i(i=1,2,…，I；j=1,2,…，J)
　　NP_mini,k≤NP_i,j,k≤NP_maxi,k(i=1,2,…，X；j=1,2,…，J；k=1,2,…,K_i)
　　上述數學模型含有連續變量(如：Q_i,j,k,HS_i,j,k)及離散變量(如：NP_i,j,k)，對于這種既含有連續變量又含有離散變量的優化問題，我們在以離散搜索法為理論依據的MDOD方法^［3］的基礎上，經改進開發了求解混合離散變量的供水系統直接優化調度軟件（用C++計算機語言），尋優結果可以直接得到1～X個泵站的運行策略，即各泵站內各種水泵的開機臺數；另外X+1～I個混合泵站，只得到泵站的最優出水流量Q_i及最優出水水壓H_i。對于這種出口流量及出口水壓已給的混合泵站優化調度問題，需對泵站內的水泵進行優化組合并確定調速泵的轉速，即二級尋優^［4、5］(由于篇幅所限，具體的求解方法另文介紹)。

　　4 實際應用

　　沈陽市日供水量達150×104 m³以上，其大小供水泵站總和有31個之多。通過對沈陽市供水系統各供水泵站的逐一分析,剔除這些供水量很少及供水量變化不大、可調余地很小及相對獨立的供水泵站，主要針對在調度及工況建模中具有實際意義的十個泵站進行研究，掌握了各泵站的水泵機組情況及水池的可調容積。沈陽市自來水公司根據沈陽市用水特點，通過多年的運行管理，摸索出了許多調度管理的經驗。他們將一天24 h分成五個各有特點的時段，分別進行調度控制，具體為：①0：00～5：00，早低峰；②5：00～8：00，早高峰；③8：00～17：00，中峰；④17：00～20：00，晚高峰；⑤20：00～24：00，晚低峰。在對沈陽市的優化調度中，以該時段劃分為基礎，提出各時段的優化調度決策方法。
　　沈陽市的供水系統主要是由定速泵站組成，另有兩個混合泵站(大伙房和新北陵泵站)，因此它屬于混合供水系統。因其供水特點較復雜，在高峰用水時有些小井泵站直接向管網供水，但水量小，難管理，不能參與調度；并且有時為限量供水，人為關啟管網及泵前閥門，這就給管網的工況建模增加了很大難度。另外，各供水泵站主要由定速泵組成，且水泵型號較為單一，有的泵站只有一種型號，并且有的泵站必須滿負荷運行，沒有多少可調余地，若采用隱式模型(進行分級優化調度)，則在尋優過程中，可能出現無解現象。因為如首先進行供水量的尋優，再進行泵站運行決策優化，則由于有些泵站可調余地較小，可能得不到可行解而使尋優中斷，由對其進行的實際測算，也證明了這一論斷。若采用式(15)的混合模型，將水源、泵站與管網有機地結合起來，從安全供水、經濟運行及供水可行性的角度出發，將含調速泵的混合泵站與定速泵站區別考慮，充分利用其各自特點，合理調配各種水泵，以達到系統整體最優，則更適合沈陽市供水系統的現有條件；因此根據其現狀，結合沈陽市調度管理方式的經驗，建立了沈陽市供水系統多目標、混合離散變量、直接優化調度模型；并根據管網的實際情況，適當放寬約束條件，以滿意解為追求目標，保證了調度軟件的
實用性。
　　利用本文建立的數學模型進行計算時，將原始數據輸入后，經優化計算輸出調度運行策略(共得五個可選方案)。經核算，所有測壓點水頭均滿足水壓要求。
　　通過計算得知，1998年3月10日利用兩種方案在部分泵站所產生的直接電費分別為：優化方案38536.383元，經驗方案41154.005 元。經實際比較發現，優化方案比經驗方案節省電費6.36%，優化方案的運行合理性是明顯的，并且其經濟效益顯著。

　　5 結論

　　本文在對供水系統優化調度時，針對不同的供水泵站采用了不同的尋優方法，由于定速泵可調余地小，泵站內可選擇的運行策略有限，宜通過一次尋優直接求解，以保證得到可行滿意解；而調速泵則通過改變水泵轉速，最大限度地滿足配水管網的水量水壓要求，進行分級優化，簡化了數學模型及求解難度，使混合離散變量直接優化模型的決策變量維數減少，提高了其計算效率，并通過二級尋優，單獨對混合泵站(含調速泵泵站)進行調度決策尋優，以充分發揮調速水泵的可調能力，可使混合泵站在最優的調度策略下運行。通過對沈陽市實際供水系統進行優化調度實踐（該課題已被驗收），其優化效果明顯。另外，由于對混合離散變量優化算法的改進，使得該優化程序的計算速度明顯提高，并且在實際運行中發現，對于配水系統的各種用水情況，該優化程序經計算后，總能找到可行的滿意解，一直沒有出現無解的情況，可見這里提出的大規模供水系統的優化調度模型及算法是有效并且可行的。

　　參考文獻：
　　［1］呂謀，張土喬，趙洪賓.供水系統的優化調度方法探討［J］.給水排水,1998，25(12).
　　［2］趙新華，田一梅，武福平.城市配水系統優化運行的研究［J］.中國給水排水，1992，8(3).
　　［3］余俊.周濟.優化方法程序庫OPB-1［M］.北京：機械工業出版社，1989.
　　［4］Lindell E O,Kevin E L.Optimal control of water supply pumpingsystems［J］.Water Resources Planning and Management,1994，120(2).
　　［5］Yung?Hsin Sun.Generalized network algorithm for water?supply?system optimization［J］.Water Resources Planning and Management，1995，121(9).

---

作者簡介：呂謀(1965-)，男，山東青島人，浙江大學副教授，博士后，研究方向：給水系統優化。
電話： (0571)7996721
E-mail: lvmoudxx@public.qd.sd.cn
收稿日期： 2000-04-20