俞國平
（同濟大學 環境科學與工程學院，上海 200092）

　　摘要：討論了管網流量分配對給水管網優化設計結果的影響，指出帶有樹枝網特征的流量分配形式在環狀給水管網設計中產生了較好的效果，研究了非線性最小費用網絡流算法用于搜索最優流量分配樹。
　　關鍵詞：流量分配；優化設計；給水管網；最小費用網絡流
　　中圖分類號：TU991.32
　　文獻標識碼：C
　　文章編號：1000-4602(2000)04-0031-03

　　在城市給水管網設計中，管道的流量分配會對設計流量產生重大影響。環狀給水管網由樹枝管道和余枝管道組成，樹枝管道構成給水管網的樹枝形供水脈絡，余枝管道則形成供水回路。比較好的流量分配形式是管網中所有的余枝管道都應取其需通過的最小流量值。然而在規模較大的給水管網中可以構造出上百萬計的樹枝網數目，其中供水最經濟的樹枝網稱之為最優流量分配樹，在此基礎上分配給余枝管道以適當的最小允許流量，便產生了一種帶有樹枝網供水特征的環狀給水管網的流量分配形式，協調供水經濟和安全的矛盾，取得較好的設計效果。

1 管網優化設計的數學模型

　　當管徑被取為設計變量時，給水管網優化設計的數學模型表達為：

　　

　　約束條件：
　　　Lh=0 　　A_q+Q=0
　　　h_i=k₃q_i^el_i/D_i^{3 　　　　D_i≥D_mini　　 i=1,2,...m_o}

　　通過水頭損失計算公式，把設計變量管徑D分解成管道流量q和管道壓降h，并略去常數項，于是原模型分解成下述兩個各有其意義的優化模型。
　　模型 1

　　

　　約束條件：
　　Lh=0
　　h＞0

　　模型２：

　　

　　約束條件：
　　Aq+Q=0
　　q_i≥q_mini
　　式中　q--管道流量?
　　　　　h--管道壓降?
　　　　　l--管道長度?
　　　　　Q--節點流量?
　　　　　n_s--水源個數?
　　　　　A--管網的銜接矩陣?
　　　　　L--管網的回路矩陣?
　　　　　H₀--控制點所需壓力標高?
　　　　　P_i--控制點到第i個水源節點的某一指定方向的沿線管道集合。
　　　　　b、e?--管道造價系數
　　　　　α、β--水力摩阻公式中的系數
　　　　　k₁、k₂、k₃--與資金回收、電價、水泵效率等因素有關的常數

　　模型1表示管道流量已知條件下，對管道壓降h進行優化設計以降低管道造價和運行費用之和。?
　　模型2表示在管道壓降不變時，對管道流量q進行最優分配計算以降低管道造價。
　　把上述兩個模型串聯起來協調地求解要比直接求解以管徑d為設計變量的優化模型容易得到逼近全域最優解的局部解。計算步驟如下：
　　① 給定初始可行流量分配q⁰，求解模型1得到最優壓降h^*；
　　② 保持h^*不變，求解模型2得到最優流量分配；
　　③ 若q^*＝q⁰，計算終止，h^*、q^*為優化設計最優解；否則，令q^*→q⁰，轉入步驟①。

2 最優流量分配樹的搜索

　　模型2改寫為：

　　

　　式中 　，是相對于第i 根管道流量的費用權重，模型2的求解就是滿足節點流量平衡方程和流量界限約束的最小費用網絡流，由于ea/β≠1，這是一個非線性網絡流問題。
　　在管道網絡中：管道被區分為樹枝和余枝，集合標記分別為B和N，其相應的管道流量分別為基本變量q^B和非基本變量qN，銜接矩陣也相應被分為A_B和A_N，節點方程表示為：
　　A_Bq^B+A_Nq^N+Q=0 　　　　　　(1)
　　q^B=-A_B^-1A_Nq^N-Q　　　　　　(2)

　　式(2)表示余枝流量已知時，即可求出樹枝流量，獨立的決策比納涼是余枝流量qN，并且：

　　 　　　　　　(3)

　　為避免計算AB的逆陣，實際計算時引用切割組矩陣表達節點流量平衡方程：

　　(C_B/C_N)(q_B/q_N)+C_QQ=0 　　　　　　　(4)

　　以圖１所示管網為例，切割組矩陣可表示為：

　　

　　由于C_B為一單位矩陣，所以有：

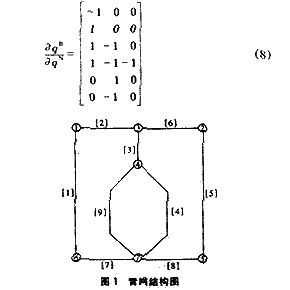
　　對于模型２中的目標函數，余枝流量的簡約梯度可表示為：

　　

　　式(9)表示余枝流量q_j的單位變化所引起的目標函數的變化。由式(8)可知q_i/q_j?可能為1、0或-1。當初始可行流量分配確定后，計算每一回路(環)的回路校正流量Δq，即可改變流量分配方案并仍然滿足流量平衡方程。
　　搜索最優流量分配樹的最小費用網絡流算法如下：
　　①確定初始可行的樹枝和余枝的區分，其指標集分別為B和N，令q_j⁰=q_min,j∈N,得到初始流量分配q₀,0→k,k為迭代指標。
　　②當迭代指標為k時，q^k為當前的流量分配，對所有余枝計算：

　　

　　③如果對所有余枝均有Rj≥0,計算終止，qk為最優流量分配，否則令
　　φ=|j|Rj=max{Rj(Rj＜0,j∈N)}
　　在第φ個回路中，令：
　　△q=min{(q_i-q_min)}|i∈B,σi＜0}
　　Φ={i|(q_i-q_min)=△q}

　　④對第φ個回路中的所有管道，計算q_i^k+1=q_i^k+σ_iΔq,得到新的流量分配，在切割組矩陣中以第φ根余枝和第Ø根樹枝互相交換進行轉軸運算，得到新的樹枝和余枝的區分集合，令k+1→k，轉入②。

3 結語

　　本文討論了管道流量分配方案對優化設計結果的影響，不同樹枝網的流量分配產生優化后的目標函數差高達14%，而把非線性最小費用網絡流算法用于尋找最小流量分配樹中得到了一定成功。每根管道的最小允許流量q_min的取值應考慮管網安全供水的復核結果，目標尚無有效方法確定q_min的取值，還需繼續研究。

---

電話：(021)65982697(O) 65981980(H)