高層建筑頂端冷卻塔的拉索預張力優化計算
方明霞1,韋林1,康治國2
(1.同濟大學工程力學研究所,上海 200092;2.上海良機冷卻塔設備有限公司,上海 201611)
摘 要: 通過求解非線性方程組,得到冷卻塔拉索的最優預張力值,使冷卻塔位于高層建筑頂端時其強度及剛度得到最優控制。
關鍵詞:最優控制;冷卻塔;拉索
中圖分類號:TQ051.5
文獻標識碼:C
文章編號:1000-4602(1999)12-0031-03
隨著城市建設的日益發展,城市中的高層、超高層建筑越來越多,有相當數量的冷卻塔被安置在高層建筑頂端。由于高處存在較強的風速 ,會使冷卻塔結構產生較大的側向位移,并提高結構的內應力值,這些位移和內應力值超過一定值后,將會使結構產生破壞。因此,在進行無風機科技冷卻塔標準結構設計(當該冷卻塔置于高層建筑頂端)時,在結構的某些部位預安置若干根拉索裝置。由于風壓高度系數增加,冷卻塔某些部位的強度與剛度可能超過設計允許值,這時可張拉預安置的拉索裝置來調節整塔的強度、剛度值,使塔體的所有部位滿足強度及剛度要求。
如何在冷卻塔產品設計時,既滿足通常產品的要求,又可在原結構的基礎上通過簡單的改進措施,最優控制冷卻塔位于高聳建筑頂端時其抗風載的能力,是非常值得研究的現實問題。
1 數學模型建立
本文選取拉索的預張力為設計變量,考察冷卻塔位于高層建筑頂端時其結構在風荷載作用下不滿足強度、剛度要求的點作為控制點。假設第j根拉索的張拉力為Xj(j=1…n) ,則第i個控制點的強度σ應滿足[1]:
![]()
式中 σi0——控制點的應力值
σij——第j根拉索張接力Xj的單位值引起該控制點的應力值
根據線性疊加原則,其疊加后的值應小于或等于允許應力值。同樣當控制量為位移時,可寫成位移控制方程:
![]()
式中 △i0——控制點的位移值
△j0——第j根拉索張拉力Xj單位值引起該控制點的位移值
如整個結構選取m個控制點,改造上述方程,并結合所有控制點的控制約束方程為:
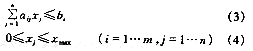
對上述結構控制約束方程進一步優化控制時,應考慮它的最優設計目標函數,而冷卻塔結構優化設計的目標函數一般應從經濟造價方面衡量,因拉索截面越小越經濟,則在滿足控制約束方程的條件下,索張拉力應盡可能小。因此寫成拉索張拉力最優控制方程為:
![]()
通過以上分析,得到利用預張力拉索來控制位于高層建筑頂端時冷卻塔結構強度及剛度的最優控制方程為:
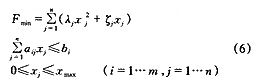
求解上述非線性規劃方程組,即可選取最佳拉索張拉力,使冷卻塔結構既可以滿足不同高度風荷載的要求,又能最大限度地滿足經濟性要求。
2 無風機科技冷卻塔的優化計算
無風機科技冷卻塔是冷卻塔行業的最新產品,以前冷卻塔結構主要以機械通風式冷卻塔為主。隨著社會和經濟的發展,節約水資源和保護環境的呼聲日益強烈,這些冷卻塔逐漸暴露一系列諸如失水量大、噪聲污染和水滴飛濺等問題。無風機科技冷卻塔以高效率的流體動能轉化裝置取代風機作為空氣動力裝置,使傳統式冷卻塔難以克服的問題迎刃而解。本文以LFCI—3000無風機科技冷卻塔為例,對其進行結構優化分析。由于該冷卻塔結構的對稱性,可以把它簡化為X-Z平面內的平面結構(圖1),從圖中可以看出各拉索的位置。
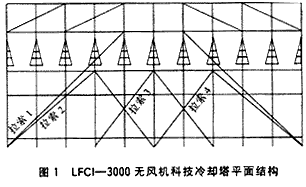
現考慮風荷載對該冷卻塔結構的影響,根據文獻[2],垂直于建筑物表面的風荷載標準值按下式計算
Wk=βzμsμzW0
式中 βz——Z高度處的風振系數
μs——風荷載體形系數
μz——風壓高度變化系數
W0——基本風壓,kN/m2
Wk——風荷載標準值,kN/m2
經動力模態分析,塔體結構的自振周期為0.17s,小于0.25s,所以取βZ=1。因無風機科技冷卻塔為矩形結構,風荷載體形系數μS取為1.3。風壓高度變化系數μZ隨著高度Z的增加而增加。根據文獻[3],若冷卻塔使用地區地面粗糙度為B類,則
μZ=(Z/10)0.32
式中 Z——冷卻塔所處高度,m?
現將冷卻塔置于100 m高層建筑的頂端,此時冷卻塔底部的μZ=2.09,用有限元法計算得:σAmax=42.29 mm,σBmax=248.4 MPa,此時冷卻塔的強度、剛度均不足。分析發現,C、D、E三點的應力也較大,故取點A為位移控制點,點B、C、D、E為應力控制點。為比較風荷載對位于不同高度冷卻塔結構的影響,表1列出10 m、100m高處控制點A的位移值及控制點B、C、D、E的應力值。
從表中可以看出,當冷卻塔位于100 m高處,在風荷載作用下其位移和應力值顯著增加。
現考慮用張緊預張力拉索的辦法來改變塔體的受力狀況。取拉索的單位預張力為1kN, 用有限 元法分別求出單位預張力作用下冷卻塔控制點A的位移值及控制點B、C、D、E的應力值,現把 計算結果列于表2。
把上述結果代入式(5),并取加權因子為1,則優化LFCI-3000冷卻塔拉索預張力的最優控制方程為:
![]()
s.t. -1.0x1-0.52x2-0.39x3-0.39x4≤-23.93
-5.824x1-6.181x2-4.888x3-4.887x4≤-33.441
-6.113x1-6.639x2-5.288x3-5.287x4≤--3.578
-6.091x1-6.631x2-5.456x3-5.307x4≤-3.462
-4.981x1-5.610x2-4.456x3-4.454x4≤-20.538
0≤x1≤12.56 0≤x2≤12.56 0≤x3≤12.56 0≤x4≤12.56
將所有規劃數據送入可求解非線性規劃方程組的二次規劃法[4]的程序中,最后求取的規劃值為:
? x={11.362 11.362 8.575 8.575}?
即當冷卻塔受到水平風荷載作用時,各拉索的最優預張力值分別為:
x1=11.362 kN,?x2=11.362 kN,
? x3=8.575 kN,? x4=8.575 kN。
這時,即能最有效地使冷卻塔位于100 m高度處滿足其強度及剛度要求。
3 結論
①對于類似于無風機科技冷卻塔的矩形框架結構,在不改變原標準結構的基礎上,用預留預張力拉索的辦法,使冷卻塔結構剛度重新分配,能最經濟地滿足冷卻塔位于高層建筑頂端時其強度及剛度要求。
②利用本文推導的冷卻塔結構強度及剛度的最優控制方程,可以求得冷卻塔拉索預張力的最優控制值。
? ③用數學模型進行有效模擬,這種大型冷卻塔拉索結構基于非線性分析的最優控制方法是可行的。
參考文獻:?
[1]張炳華等.土建結構優化設計[M].上海:同濟大學出版社,1998.
[2]中國建筑工業出版社.結構工程師常用規范選[S].北京:中國建筑工業出版 社,1994.
[3]張相庭.工程抗風設計計算手冊[M].北京:中國建筑工業出版社,1998.
[4]韋林,姜宏偉.群樁擴張位移的最優控制分析[J].江西工 業大學學報,1991,13(2):611-615.
電 話:(021)65116755(H) 65983591(O)
傳 真:(021)65116755?
E-mail:fangmxch@online.sh.cn
收稿日期:1999-05-14
論文搜索
月熱點論文
論文投稿
很多時候您的文章總是無緣變成鉛字。研究做到關鍵時,試驗有了起色時,是不是想和同行探討一下,工作中有了心得,您是不是很想與人分享,那么不要只是默默工作了,寫下來吧!投稿時,請以附件形式發至 paper@h2o-china.com ,請注明論文投稿。一旦采用,我們會為您增加100枚金幣。








